Trong mặt phẳng toạ độ Oxy, cho parabol (P): y = x^2 và đường thẳng d: y=2x+|m|+ 1 ( m là tham số ). a) Chứng minh đường thẳng ở luôn cắt (P) tại 2 điểm phân biệt. b) Tìm m để đường thẳng d cắt (P) tại 2 điểm phân biệt có hoành độ x1 x2
a: PTHĐGĐ là:
x^2-2x-|m|-1=0
a*c=-|m|-1<0
=>(d)luôn cắt (P) tại hai điểm phân biệt
b: Bạn bổ sung lại đề đi bạn
Trong mặt phẳng toạ độ Oxy,cho parabol(P):y=-x2 và đường thẳng (d) đi qua điểm I(0;1) có hệ số góc k
Viết phương trình đường thẳng (d).Chứng minh rằng :Với mọi giá trị của k, đường thẳng (d) luôn cắt parabol(P) tại hai điểm phân biệt A và B
Trên mặt phẳng tọa độ Oxy cho parabol (P): y=x2 và đường thẳng (d): y=2mx+1 (m là tham số)
1) Chứng minh rằng với mọi m thì đường thẳng (d) và parabol (P) cắt nhau tại 2 điểm phân biệt.
2) Gọi giao điểm của đường thẳng (d) và parabol (P) là A và B. Chứng minh tam giác OAB vuông.
Trong mặt phẳng toạ độ Oxy, cho parabol \(\left(P\right):y=x^2\) và đường thẳng \(\left(d\right):y=2x+3\)
1) Chứng minh rằng (d) và (P) có hai điểm chung phân biệt.
2) Gọi A và B là các điểm chung của (d) và (P). Tính diện tích tam giác OAB ( O là gốc toạ độ )
Lời giải:
1)
Xét pt hoành độ giao điểm:
\(x^2-(2x+3)=0\)
\(\Leftrightarrow x^2-2x-3=0\)
\(\Leftrightarrow (x-3)(x+1)=0\Leftrightarrow \left[\begin{matrix} x=3\\ x=-1\end{matrix}\right.\)
PT hoành độ giao điểm có hai nghiệm pb nên hai đths cũng cắt nhau tại hai điểm phân biệt hay nó có hai điểm chung phân biệt (đpcm)
2)
Không mất tổng quát giả sử \(x_A=3, x_B=-1\)
\(\Rightarrow y_A=9; y_B=1\)
\(\Rightarrow OA=\sqrt{(x_A-0)^2+(y_A-0)^2}=3\sqrt{10}\)
\(OB=\sqrt{(x_B-0)^2+(y_B-0)^2}=\sqrt{2}\)
\(AB=\sqrt{(x_A-x_B)^2+(y_A-y_B)^2}=4\sqrt{5}\)
Áp dụng công thức Herong với $p$ là nửa chu vi, $a=OA, b=OB,c=AB$ thì:
\(S_{OAB}=\sqrt{p(p-a)(p-b)(p-c)}=6\) (đơn vị diện tích)
Trong mặt phẳng toạ độ cho parabol y=x^2 và đường thẳng y=2mx-m^2+m-1
.
a. Tìm toạ độ giao điểm của (P) và (d) khi .
b. Tìm để (P) cắt (d) tại hai điểm phân biệt.
c. Tìm để (P) và (d) có một điểm chung duy nhất.
d. Tìm để (P) cắt (d) tại điểm có hoành độ bằng 2.
Trong mặt phẳng tọa độ Oxy, cho parabol (P): y=x2 và đường thẳng (d): y=2(m-1)x+5-2m (m là tham số)
a) Vẽ đồ thị parabol (P).
b) Biết đường thẳng (d) luôn cắt parabol (P) tại hai điểm phân biệt. Gọi hoành độ giao điểm của đường thẳng (d) và parabol (P) là x1, x2. Tìm m để x+x=6
b) Phương trình hoành độ giao điểm của (P) và (d) là:
\(x^2=2\left(m-1\right)x+5-2m\)
\(\Leftrightarrow x^2-2\left(m-1\right)x-5+2m=0\)
Áp dụng hệ thức Vi-et, ta được:
\(x_1+x_2=2\left(m-1\right)\)
Ta có: \(x_1+x_2=6\)
\(\Leftrightarrow2\left(m-1\right)=6\)
\(\Leftrightarrow m-1=3\)
hay m=4
Vậy: m=4
Trong mặt phẳng toạ độ Oxy , cho parabol (P): y= x2 và đường thẳng (d):y= (2m-3)x-m2+3m. a) Chứng minh đường thẳng(d) luôn cắt (P)tại hai điểm phân biệt có hoành độ là x1,x2. b) Tìm tất cả các giá trị nguyên của m để trị tuyệt đối x1+ trị tuyệt đối x2 = 3
a: PTHĐGĐ là;
x^2-(2m-3)x+m^2-3m=0
Δ=4m^2-12m+9-4m^2+12m=9>0
=>(P) luôn cắt (d) tại hai điểm pb
b: |x1|+|x2|=3
=>x1^2+x2^2+2|x1x2|=9
=>(2m-3)^2-2(m^2-3m)+2|m^2-3m|=9
TH1: m>=3 hoặc m<=0
=>(2m-3)^2=9
=>m=3(nhận) hoặc m=0(nhận)
Th2: 0<m<3
=>4m^2-12m+9-4(m^2-3m)=9
=>4m^2-12m-4m^2+12m=0
=>0m=0(luôn đúng)
Trong mặt phẳng toa độ Oxy cho parabol(P): y=x^2 và đường thẳng (d): y=kx+1.
1:Chứng minh rằng đường thẳng (d) luôn cắt parabol (P) tại hai điểm phân biệt với mọi k
2: gia sử (d) cắt (P) tại E và F, gọi hoành độ của E và F lần lượt là x và y. Tính M= |x - y|
Giải bài này hộ tui với
Trong mặt phẳng tọa độ Oxy,cho Parabol (P):y=x^2 và đường thẳng (d): y=2x-m+1 (m là tham số)
a) Tìm tọa độ giao điểm của (d) và (P) khi m=2
b) Tìm M để đường thẳng (d) cắt Parabol (P) tại hai điểm phân biệt có tung độ là y1,y2 thỏa mãn
b: Thay m=2 vào (d), ta được:
y=2x-2+1=2x-1
Phương trình hoành độ giao điểm là:
\(x^2=2x-1\)
=>\(x^2-2x+1=0\)
=>(x-1)^2=0
=>x-1=0
=>x=1
Thay x=1 vào (P), ta được:
\(y=1^2=1\)
Vậy: Khi m=2 thì (P) cắt (d) tại A(1;1)
b: Phương trình hoành độ giao điểm là:
\(x^2=2x-m+1\)
=>\(x^2-2x+m-1=0\)
\(\text{Δ}=\left(-2\right)^2-4\cdot1\cdot\left(m-1\right)\)
=4-4m+4
=-4m+8
Để (P) cắt (d) tại hai điểm phân biệt thì Δ>0
=>-4m+8>0
=>-4m>-8
=>m<2
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2\\x_1x_2=\dfrac{c}{a}=m-1\end{matrix}\right.\)
y1,y2 thỏa mãn gì vậy bạn?
Trong mặt phẳng toạ độ Oxy, cho parabol (P) y=x^2 và đường thẳng (d) y=x+2.
a) vẽ parabol (P) và đường thẳng (d) trên cùng mặt phẳng toạ độ Oxy.
b) Tìm toạ độ giao điểm của (P) và (d) bằng phép tính.
c) viết phương trình đường thẳng (d') có dạng y=ax+b , biết (d') song song với (d) và đi qua điểm M(2:5)
`a)`
`@ O(0;0), A(1;1), B(-1;1) in (P)`
`@ C(0;2), D(-2;0) in (d)`
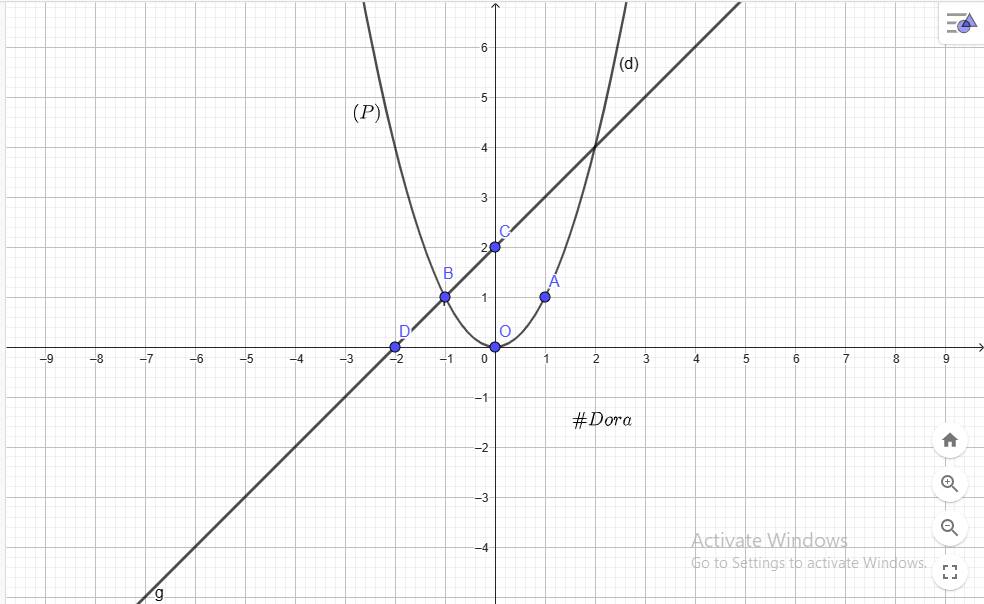
`b)` Ptr hoành độ của `(P)` và `(d)` là:
`x^2=x+2`
`<=>x^2-x-2=0`
Ptr có: `a-b+c=1+1-2=0`
`=>x_1=-1;x_2=-c/a=2`
`=>y_1=1;y_2=4`
`=>(-1;1), (2;4)` là giao điểm của `(P)` và `(d)`
`c)` Vì `(d') //// (d)=>a=1` và `b ne 2`
Thay `a=1;M(2;5)` vào `(d')` có:
`5=2+b<=>b=3` (t/m)
`=>` Ptr đường thẳng `(d'): y=x+3`
