Cho tứ giác ABCD có hai đường chéo cắt nhau ở I. Biết AB = ID = 6cm, IA = 8cm, IB = 4cm. Tính độ dài AD

Những câu hỏi liên quan
cho honhf bình hành abcd có ab=8cm, ad=6cm, trên cạnh bc lấy điểm m sao cho bm=4cm. đường thẳng am cắt đường chéo bd tại i cắt đường thẳng dc tại n
tính tỉ số ib/id, chứng minh tam giác mab, tam giác and đồng dạng ; tính độ dài dn và cn; chứng minh ia=im*in
Cho hình bình hành ABCD có AB= 8cm ,AD=6cm. Trên cạnh BC lấy điểm M sao cho BM=4cm. Đường thẳng AM cắt đường chéo BD tại I, cắt đường thẳng BC tại N.
a. tính tỉ số IB = ID
b. CM: Tam giác AMB đồng dạng tam giác AND. Tính độ dài DN và CN
c. CM . IA^2 = IM.IN
Cho tứ giác ABCD có I là giao điểm của hai đường chéo . tính AD biết AB = 6 ; IA = 8 ; IB = 4 ; ID = 6
Tam giác ABI có cạnh AB < AI => góc ABI > góc AIB
Kẻ AH vuông góc với BD . Đặt BH = x; AH = y
+) Nếu H nằm trong đoạn BI
Áp dụng ĐL Pi ta go trong tam giác vuông AHB có: AH2 + BH2 = AB2 => y2 + x2 = 36 (1)
HI = 4 - x
Áp dụng ĐL Pi ta go trong tam giác vuông AHI có: AH2 + HI2 = AI2 => y2 + (4 - x)2 = 64 => y2 + x2 + 16 - 8x = 64 (2)
Từ (1)(2) => 36 + 16 - 8x = 64 => 8x = -12 => Loại
=> H nằm ngoài đoạn BI về phía B
HI = x + 4
Áp dụng ĐL Pi ta go trong tam giác vuông AHI có: AH2 + HI2 = AI2 => y2 + (x+ 4)2 = 64 => y2 + x2 + 8x + 16 = 64 (3)
Từ (1)(3) => 36 + 16 + 8x = 64 => 8x = 12 => x = 1,5
=> y2 = 33,75
HD = x + 4 + 6 = 11,5
Áp dụng ĐL Pita go trong tam giác vuông AHD có: AD2 = y2 + HD2 => AD2 = 33,75 + 11,52 = 166 => AD = \(\sqrt{166}\approx12,88\) (cm)
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD có
A
B
8
c
m
,
A
D
6
c
m
.
Trên cạnh BC lấy M sao cho BM 4cm. Đường thẳng AM cắt đường chéo BD tại I, cắt đường thẳng DC tại N.a) Tính tỉ số IB/IDb) Chứng minh ΔMAB và ΔAND đồng dạngc) Tính độ dài DN và CNd) Chứng minh
I
A
2
...
Đọc tiếp
Cho hình bình hành ABCD có A B = 8 c m , A D = 6 c m . Trên cạnh BC lấy M sao cho BM = 4cm. Đường thẳng AM cắt đường chéo BD tại I, cắt đường thẳng DC tại N.
a) Tính tỉ số IB/ID
b) Chứng minh ΔMAB và ΔAND đồng dạng
c) Tính độ dài DN và CN
d) Chứng minh I A 2 = I M . I N
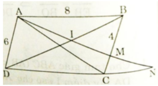
a) AD // BC (gt)![]()
b) Xét ΔAMB và ΔNAD có:
∠BAM = ∠ AND (so le trong, AB // CD)
∠ABM = ∠ADN (góc đối của hình bình hành)
⇒ ΔAMB ∼ ΔNAD (g.g)
c) ΔAMB ∼ ΔNAD (cmt)
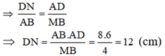
Do đó: CN = DN – DC = 12 – 8 = 4 (cm)
d) Do AB //CD nên theo hệ quả định lí Ta-lét, ta có
![]()
Tương tự, do AD // BM nên
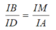
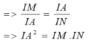
Đúng 0
Bình luận (0)
Tứ giác ABCD có AD và BC cắt nhau tại O, AB =6cm, OA=8cm, OB=4cm, OD=6cm . Tính độ dài AD
Ai làm được mình tick cho
Cho hình bình hành ABCD có AB = 8cm, AD = 6cm. Trên cạnh BC lấy M sao cho BM = 4cm. Đường thẳng AM cắt đường chéo BD tại I, cắt đường thẳng DC tại N.a) Tính tỉ số IB/IDb) Chứng minh ΔMAB và ΔAND đồng dạngc) Tính độ dài DN và CNd) Chứng minh IA2 = IM.IN
đây là toán lớp 8 mà
tứ giác ABCD có hai đường chéo vuông góc và AB=8cm, BC=7cm, AD=4cm. tính độ dài CD=?
Xet tam giac AOB OA^2+OB^2=AB^2
CM Tuong Tu: OD^2=AD^2-OA^2 :OC^2=BC^2-OB^2 (1)
Co DC^2=OD^2+OC^2 (2)
Thay (1) vao (2)Ta duoc
AD^2+BC^2-(OA^2+OB^2)=DC^2 =>4^2+7^2-8^2=DC^2=>DC=1cm
Đúng 0
Bình luận (0)
Tứ giác ABCD có hai đường chéo vuông góc và AB = 8cm, BC = 7cm, AD = 4cm. Tính độ dài CD.
Kí hiệu: OA=a, OB=b, OC=c, OD=d
Áp dụng định lí Py-ta-go cho các tam giác vuông tại O ta có:
a^2+b^2=8^2=64
b^2+c^2=7^2=49 (1)
a^2+d^2=4^2=16 (2)
Từ (1) và (2): a^2+b^2+c^2+d^2=65
=> c^2+d^2=65-64=1
Mà CD^2=c^2+d^2=1
=> CD=1cm
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có O là giao điểm của 2 đường chéo, AB=6cm, OA=8cm, OB=4cm, OD=6cm. Tính AD

















