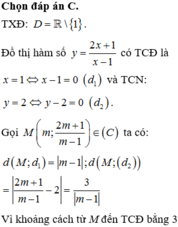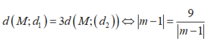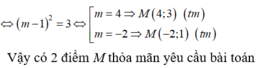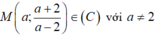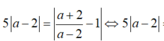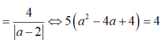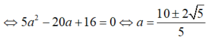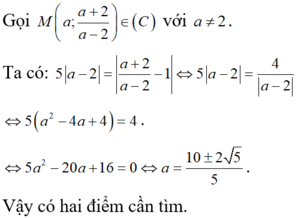Cho hàm số y = \(\frac{2x+1}{x-1}\)có đò thị (C). Có bao nhiêu điểm m thuộc (C) có tung độ nguyên dương sao cho khoảng cách từ M đến tiệm cận đứng =3 lần khoảng cách từ M đến tiệm cận ngang của đồ thị (C)

Những câu hỏi liên quan
Cho hàm số
y
2
x
+
1
x
-
1
có đồ thị (C). Có bao nhiêu điểm M thuộc (C) có tung độ nguyên dương sao cho khoảng cách từ M đến tiệm cận đứng bằng 3 lần khoảng cách từ M đến tiệm cận ngang của đồ thị (C) A. 0 B. 3 C. 2 D. 1
Đọc tiếp
Cho hàm số y = 2 x + 1 x - 1 có đồ thị (C). Có bao nhiêu điểm M thuộc (C) có tung độ nguyên dương sao cho khoảng cách từ M đến tiệm cận đứng bằng 3 lần khoảng cách từ M đến tiệm cận ngang của đồ thị (C)
A. 0
B. 3
C. 2
D. 1
Cho hàm số
y
2
x
+
1
x
-
1
có đồ thị (C) . Có bao nhiêu điểm M thuộc (C) có tung độ nguyên dương sao cho khoảng cách từ M đến tiệm cận đứng bằng 3 lần khoảng cách từ M đến tiệm cận ngang của đồ thị (C). A. 0 B. 3 C. 2 D. 1
Đọc tiếp
Cho hàm số y = 2 x + 1 x - 1 có đồ thị (C) . Có bao nhiêu điểm M thuộc (C) có tung độ nguyên dương sao cho khoảng cách từ M đến tiệm cận đứng bằng 3 lần khoảng cách từ M đến tiệm cận ngang của đồ thị (C).
A. 0
B. 3
C. 2
D. 1
Có bao nhiêu điểm M thuộc đồ thị (C) của hàm số y
x
+
2
x
-
2
sao cho khoảng cách từ điểm M đến tiệm cận ngang bằng 5 lần khoảng cách từ M đến tiệm cận đứng? A. 2. B. 1 C. 3. D. 4.
Đọc tiếp
Có bao nhiêu điểm M thuộc đồ thị (C) của hàm số y = x + 2 x - 2 sao cho khoảng cách từ điểm M đến tiệm cận ngang bằng 5 lần
khoảng cách từ M đến tiệm cận đứng?
A. 2.
B. 1
C. 3.
D. 4.
Có bao nhiêu điểm M thuộc đồ thị (C) của hàm số
y
x
+
2
x
−
2
sao cho khoảng cách từ điểm M đến tiệm cận ngang bằng 5 lần khoảng cách từ M đến tiệm cận đứng? A. 2 B. 1 C. 3 D. 4
Đọc tiếp
Có bao nhiêu điểm M thuộc đồ thị (C) của hàm số y = x + 2 x − 2 sao cho khoảng cách từ điểm M đến tiệm cận ngang bằng 5 lần khoảng cách từ M đến tiệm cận đứng?
A. 2
B. 1
C. 3
D. 4
Cho hàm số y = x + 2 x - 3 có đồ thị (C). Có bao nhiêu tiêu điểm thuộc sao cho khoảng cách từ điểm đến tiệm cận ngang bằng 5 lần khoảng cách từ điểm đến tiệm cận đứng.
A. 1
B. 2
C. 3
D. 4
Tìm điểm M trên đồ thị của hàm số sao cho khoảng cách từ M đến tiệm cận đứng bằng khoảng cách từ M đến tiệm cận ngang.Đồ thị (C) của hàm số
y
x
+
2
x
-
3
Đọc tiếp
Tìm điểm M trên đồ thị của hàm số sao cho khoảng cách từ M đến tiệm cận đứng bằng khoảng cách từ M đến tiệm cận ngang.
Đồ thị (C) của hàm số y = x + 2 x - 3
Giả sử M( x o ; y o ) ∈ (C). Gọi d 1 là khoảng cách từ M đến tiệm cận đứng và d 2 là khoảng cách từ M đến tiệm cận ngang, ta có:
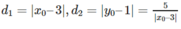
Có hai điểm thỏa mãn đầu bài, đó là hai điểm có hoành độ x o = 3 + 5 hoặc x o = 3 - 5
Đúng 0
Bình luận (0)
cho hàm số \(y=\dfrac{x+2}{x-3}\left(C\right)\). Có tất cả bao nhiêu điểm M thuộc (C) sao cho khoảng cách từ M đến tiệm cận ngang bằng 5 lần khoảng cách từ M đến tiệm cận đứng.
Hàm nhận \(x=3\) là tiệm cận đứng và \(y=1\) là tiệm cận ngang
Gọi \(M\left(a;b\right)\Rightarrow b=\dfrac{a+2}{a-3}\)
Khoảng cách đến tiệm cận đứng: \(\left|x_M-3\right|=\left|a-3\right|\)
Khoảng cách đến tiệm cận ngang: \(\left|y_M-1\right|=\left|b-1\right|\)
Ta có hệ: \(\left\{{}\begin{matrix}b=\dfrac{a+2}{a-3}\\\left|b-1\right|=5\left|a-3\right|\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}M\left(4;6\right)\\M\left(2;-4\right)\end{matrix}\right.\) có 2 điểm
Đúng 1
Bình luận (0)
Cho hàm số \(y=\frac{x+2}{x-3}\). Tìm trên đồ thị của hàm số điểm M sao cho khoảng cách từ M đến tiệm cận đứng bằng khoảng cách từ M đến tiệm cận ngang.
Xét \(M\left(m;1+\frac{5}{m-3}\right)\) thuộc đồ thị đã cho
Theo yêu cầu bài tài <=> \(\left|m-3\right|=\left|\frac{5}{m-3}\right|\Leftrightarrow m=3\pm\sqrt{5}\)
Vậy \(M\left(3\pm\sqrt{5};1\pm\sqrt{5}\right)\)
Đúng 0
Bình luận (0)
Tọa độ điểm M thuộc đồ thị (C) của hàm số y
2
x
-
1
x
-
1
sao cho khoảng cách từ điểm M đến tiệm cận đứng bằng 1 là A. B. C. D.
Đọc tiếp
Tọa độ điểm M thuộc đồ thị (C) của hàm số y = 2 x - 1 x - 1 sao cho khoảng cách từ điểm M đến tiệm cận đứng bằng 1 là
A. ![]()
B. ![]()
C. 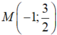
D. 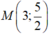
Đáp án A
Gọi
 với
a
≢
1
.
với
a
≢
1
.
Tiệm cận đứng của (C) là x-1.
Ta có 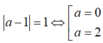 . Vậy
. Vậy ![]() .
.
Đúng 0
Bình luận (0)