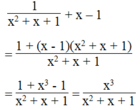
Biểu thức bằng 0 khi x 3  = 0 và x 2 + x + 1 ≠ 0

Ta có:  x 3  = 0 ⇒ x = 0;

x 2 + x + 1 = x 2 + 2 . x . 1 / 2 + 1 / 4 + 3 / 4 = x + 1 / 2 2 + 3 / 4 ≠ 0 mọi x.

Vậy với x = 0 thì giá trị của biểu thức bằng 0.

\(\frac{3x-7}{21}-\frac{x\left(x-2\right)}{7}\le\frac{x-2}{3}-\frac{x\left(x+1\right)}{7}\)

\(\Leftrightarrow\frac{3x-7}{21}-\frac{3x\left(x-2\right)}{21}\le\frac{7x-14-3x\left(x+1\right)}{21}\)

\(\Leftrightarrow3x-7-3x^2+6x\le7x-14-3x^2-3x\)

\(\Leftrightarrow9x-7\le4x-14\Leftrightarrow5x\le-7\Leftrightarrow x\le-\frac{7}{5}\)

vậy tập nghiệm của bft là S = { x | x =< -7/5 } 

\(\frac{3x-7}{21}-\frac{x\left(x-2\right)}{7}\le\frac{x-2}{3}-\frac{x\left(x+1\right)}{7}\)

\(< =>\frac{3x-7}{21}-\frac{3x\left(x-2\right)}{21}\le\frac{7\left(x-2\right)}{21}-\frac{3x\left(x+1\right)}{21}\)

\(< =>3x-7-3x^2+6x\le7x-14-3x^2+3x\)

\(< =>-3x^2+3x+9x-7-10x+14\le0\)

\(< =>-x-7\le0\)

\(< =>x+7\ge0< =>x\ge-7\)

vậy với x >= -7 thì ....

Biểu thức xác định khi: x 2 - 4 = x + 2 x - 2 ≠ 0 và x + 2 2 ≠ 0 hay x ≠ ± 2

Ta có:

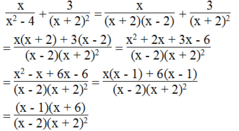
Biểu thức bằng 0 khi (x – 1)(x + 6) = 0 và x - 2 x + 2 2 ≠ 0

+) Ta có: (x - 1).(x + 6) = 0 khi x - 1= 0 hay x + 6 = 0

x - 1 = 0 khi x = 1 ( thỏa mãn điều kiện)

x + 6 = 0 khi x = -6 ( thỏa mãn điều kiện)

Vậy với x = 1 hoặc x = - 6 thì giá trị biểu thức bằng 0.

là sao ko hiểu cái đề

ko hiểu đề bài

 \(A=\frac{7-X}{X-10}\left(X\inℤ\right)\)

A) ĐỂ A CÓ NGHĨA => X - 10 ≠ 0 => X ≠ 10

B) ĐỂ A > 0

=> \(\frac{7-X}{X-10}>0\)

XÉT HAI TRƯỜNG HỢP :

1. \(\hept{\begin{cases}7-X>0\\X-10>0\end{cases}}\Leftrightarrow\hept{\begin{cases}-X>-7\\X>10\end{cases}}\Leftrightarrow\hept{\begin{cases}X< 7\\X>10\end{cases}}\)( LOẠI )

2. \(\hept{\begin{cases}7-X< 0\\X-10< 0\end{cases}}\Leftrightarrow\hept{\begin{cases}-X< -7\\X< 10\end{cases}}\Leftrightarrow\hept{\begin{cases}X>7\\X< 10\end{cases}}\Leftrightarrow7< X< 10\)

VẬY VỚI 7 < X < 10 THÌ A > 0

ĐKXĐ \(\hept{\begin{cases}x\ne0\\x\ne\pm1\end{cases}}\)

với ĐKXĐ ta có

=\(\left(\frac{x^2+2x+1-x^2+2x-1}{\left(x+1\right)\left(x-1\right)}\right):\frac{2x}{7\left(x-1\right)}\)

=\(\frac{4x}{\left(x+1\right)\left(x-1\right)}\times\frac{7\left(x-1\right)}{2x}\)

=\(\frac{14}{x+1}\)

b, x=6(t/m)

khi x=6 thì A=\(\frac{14}{6+1}=2\)

c,A=7<=>\(\frac{14}{x+1}=7\)

         \(\Leftrightarrow7x+7=14\)

           \(\Leftrightarrow7x=7\Leftrightarrow x=1\left(loại\right)\)

Vậy ko có giá trị x để A=7

a) Giá trị của \(\frac{x}{x^2-4}+\frac{3}{\left(x+2\right)^2}\) được xác định

\(\Leftrightarrow x^2-4\ne0\)

\(\Leftrightarrow\left(x-2\right)\left(x+2\right)\ne0\)

\(\Leftrightarrow\hept{\begin{cases}x-2\ne0\\x+2\ne0\end{cases}}\)

\(\Leftrightarrow x\ne\pm2\)

b) Giá trị của biểu thức bằng 0

\(\Leftrightarrow\frac{x}{x^2-4}+\frac{3}{\left(x+2\right)^2}=0\)

\(\Leftrightarrow\frac{x}{\left(x+2\right)\left(x-2\right)}+\frac{3}{\left(x+2\right)^2}=0\)

\(\Leftrightarrow\frac{x\left(x+2\right)+3\left(x-2\right)}{\left(x-2\right)\left(x+2\right)^2}=0\)

\(\Leftrightarrow x^2+2x+3x-6=0\)

\(\Leftrightarrow x^2+6x-x-6=0\)

\(\Leftrightarrow x\left(x+6\right)-\left(x+6\right)=0\)

\(\Leftrightarrow\left(x+6\right)\left(x-1\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}x+6=0\\x-1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-6\\x=1\end{cases}}}\)( Thỏa mãn điều kiện xác định )

Vậy ......................