Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC (H thuộc BC). Biết AB=6cm,AC=8cm.Tính AH,HB,HC

Những câu hỏi liên quan
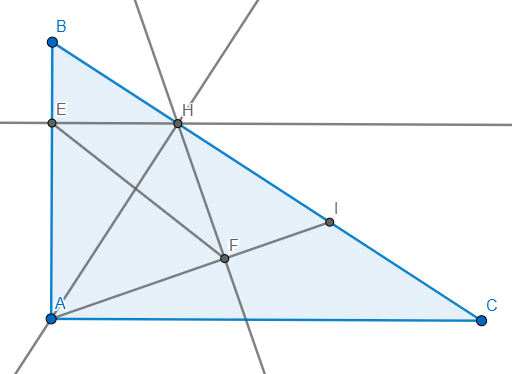
Cho tam giác ABC vuông tại A,đường cao AH(H thuộc BC) 1/Giả sử AB=6cm,AC=8cm.Tính độ dài BC,AH 2/Kẻ HE vuông góc với AB tại E.Gọi I là trung điểm của HC.Kẻ HF vuông góc với AI tại F. Chứng minh tam giác AEF đồng dạng với tam giác AIB.
a) tam giác ABC vuông tại A nên áp dụng Py-ta-go:
\(\Rightarrow BC^2=AB^2+AC^2=6^2+8^2=100\Rightarrow BC=10\left(cm\right)\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{6.8}{10}=4.8\left(cm\right)\)
b) tam giác AHB vuông tại H có đường cao HE nên áp dụng hệ thức lượng
\(\Rightarrow AE.AB=AH^2\)
tam giác AHI vuông tại H có đường cao HF nên áp dụng hệ thức lượng
\(\Rightarrow AF.AI=AH^2\Rightarrow AF.AI=AE.AB\Rightarrow\dfrac{AF}{AB}=\dfrac{AE}{AI}\)
Xét \(\Delta AEF\) và \(\Delta AIB:\) Ta có: \(\left\{{}\begin{matrix}\dfrac{AE}{AI}=\dfrac{AF}{AB}\\\angle BAIchung\end{matrix}\right.\)
\(\Rightarrow\Delta AEF\sim\Delta AIB\left(c-g-c\right)\)
Đúng 1
Bình luận (0)
1: Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot10=6\cdot8=48\)
hay AH=4,8(cm)
Đúng 0
Bình luận (0)
cho tam giác abc cân tại a có AB=AC=5cm, BC=8cm. kẻ AH vuông góc với BC (H thuộc BC) a) chứng minh HB=HC và góc BAH= góc CAH. b) tính độ dài AH. c) kẻ HD vươong góc với AB (D thuộc AB), kẻ HE vuông góc với AC (E thuộc AC). Chứng minh tam giác HDE là tam giác cân
a: Ta có: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
hay HB=HC
Ta có: ΔABC cân tại A
mà AH là đường cao
nên AH là đường phân giác
hay \(\widehat{BAH}=\widehat{CAH}\)
b: BH=CH=BC/2=4(cm)
nên AH=3(cm)
c: Xét ΔAEH vuông tại E và ΔADH vuông tại D có
AH chung
\(\widehat{EAH}=\widehat{DAH}\)
DO đó: ΔAEH=ΔADH
Suy ra: HE=HD
hay ΔHDE cân tại H
Đúng 3
Bình luận (1)
cho tam giác ABC cân tại A, kẻ đường cao AH (H thuộc BC)
a/ chứng minh : tam giác AHB= tam giác AHC
b/chứng minh : HB=HC và góc BAH=góc CAH
c/ cho BC=20cm, AB = 8cm.tính độ dài đoạn thẳng AH
d/ kẻ HD vuông góc AB (D thuộc AB), HE vuông góc AC ( E thuộc AC). chứng minh rằng tam giác HDE là tam giác cân
e/ chứng minh rằng DE//BC
1, Tam giác ABC vuông tại A, kẻ đường cao AH
a.Tính AB, AC,BC, HC nếu AH= 6cm, BH= 4,5cm
b.Biết AB= 6cm, HB- 3cm. Tính AH, AC,CH
5, Cho tam giác ABC vuông tại A có AB=21cm, góc C= 40 độ
a.Tính AC
b,Tính BC
Bài 5:
a) Xét ΔABC vuông tại A có
\(AC=AB\cdot\cot\widehat{C}\)
\(=21\cdot\cot40^0\)
\(\simeq25,03\left(cm\right)\)
b) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=21^2+25,03^2=1067,5009\)
hay \(BC\simeq32,67\left(cm\right)\)
Đúng 1
Bình luận (0)
Cho tam giác ABC có AB=AC=5cm;BC=6cm. Kẻ AH vuông góc BC(H thuộc BC)
a. Chứng minh HB=HC và góc BAH=góc CAH
b. Tính độ dài AH
c. Kẻ HD vuông góc AB (D thuộc AB); HE vuông góc AC (E thuộc AC). Chứng minh tam giác ADE cân.
d. Chứng minh DE song song BC
Làm giúp mình nha
Cho tam giác ABC cân có AB=AC=5cm, BC= 8cm.Kẻ AH vuông góc với BC ( H thuộc BC). a, Chứng minh HB=HC b, Tính độ dài AH. c, Kẻ HD vuông góc với AB(D thuộc AB), kẻ HE vuông góc với AC ( E thuộc AC).Chứng minh tam giác HDE cân. d, CM: AH là đường trung trực của đoạn thẳng DE ( giúp mk vs mai mk phải nộp rồi)
a.ta có trong tam giác cân ABC đường cao cũng là đường trung tuyến => HB = HC
b.áp dụng định lý pitago ta có:
\(AB^2=AH^2+HB^2\)
\(5^2=AH^2+\left(8:2\right)^2\)
\(AH=\sqrt{5^2-4^2}=3cm\)
c.Xét tam giác vuông BHD và tam giác vuông CHE, có:
BH = CH ( cmt )
góc B = góc C ( ABC cân )
Vậy tam giác vuông BHD = tam giác vuông CHE
=> HD = HE
=> HDE cân tại H
d.ta có AB = AD + DB
AC = AE + EC
Mà BD = CE ( 2 cạnh tương ứng của 2 tam giác bằng nhau )
=> AD = AE
=> ADE cân tại A
Mà A là đường cao cũng là đường trung trực trong tam giác cân ABC cũng là đường trung trực của tam giác cân ADE ( cmx )
Chúc bạn học tốt !!!!
Đúng 3
Bình luận (0)
cho tam giác ABC cân tại A , kẻ AH vuông góc với BC ( H thuộc BC)
a)chứng minh HB =HC
b)kẻ HD vuông góc với AB ( D thuộc AB) và HE vuông góc với AC ( E thuộc AC) . Chứng minh tam giác HDE cân
Cho tam giác ABC vuông tại a có đường cao AH 1.cho biết AB =3cm , AC=4cm , tính độ dài các đoạn BC,HB,HC,AH 2. Kẻ HE vuông góc với AB , HF vuông góc với AC ( E thuộc AB , F thuộc AC )
a: BC=5cm
AH=2,4cm
BH=1,8cm
CH=3,2cm
Đúng 0
Bình luận (0)
cho tam giác abc vuông tại a. kẻ ah vuông góc với bc (h thuộc bc). tính ah, biết hb=2cm, hc=8cm

















