tìm x:
a.(x+1)^4=16
b.(x-1)^4=16
Những câu hỏi liên quan
1) tìm số tự nhiên x biết :
a) 16, x - 2^4 . 3 = 4^3
b) 16 < 4 ^ x + 1 < 4 ^4
2.tìm số tự nhiên x biết :
a) 16 x - 2^4 . 3 = 4^3
b) 16 < 4^ x + 1 < 4^4
Cho biểu thức A = \(\dfrac{x+4}{\sqrt{x}+4}\) ; B = \(\left(\dfrac{x+3\sqrt{x}-3}{x-16}-\dfrac{1}{\sqrt{x}+4}\right):\dfrac{\sqrt{x}+1}{\sqrt{x}-4}\)
x ≥ 0, x ≠ 16
a) Rút gọn
b) Tìm giá trị nhỏ nhất của biểu thức \(\dfrac{A}{B}\)
(mink đag cần gấp)
a) Ta có: \(B=\left(\dfrac{x+3\sqrt{x}-3}{x-16}-\dfrac{1}{\sqrt{x}+4}\right):\dfrac{\sqrt{x}+1}{\sqrt{x}-4}\)
\(=\left(\dfrac{x+3\sqrt{x}-3-\sqrt{x}+4}{\left(\sqrt{x}+4\right)\left(\sqrt{x}-4\right)}\right):\dfrac{\sqrt{x}+1}{\sqrt{x}-4}\)
\(=\dfrac{x+2\sqrt{x}+1}{\left(\sqrt{x}+4\right)\left(\sqrt{x}-4\right)}\cdot\dfrac{\sqrt{x}-4}{\sqrt{x}+1}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}+4}\)
Đúng 1
Bình luận (0)
Tìm x:
a, (x+1/2) + (x+1/4) + (x+1/8) + (x+1/16)=23/16
b, x*(1/2+1/3+1/6)=425
a x * 4 + [1/2 + 1/4 + 1/8 + 1/6] = 23/16
x * 4 + 25/24 = 23/16
x * 4 = 23/16 - 25/24
x * 4 = 38/96 = 19/48
x = 19/48 / 4
x = 19/172
b x * 1 = 425
x = 425 / 1
x = 425
Đúng 0
Bình luận (0)
Bài 2: Tìm x, biết: a) (x+2)(x² -2x+4)-x(x²+2)=15 b) (x-2)³-(x-4)(x² + 4x+16) + 6(x+1)=49 c) (x - 1)³ + (2 - x)(4 + 2x + x²)+ 3x(x + 2) = 16 d) (x - 3)³ - (x - 3)(x² + 3x + 9) + 9(x + 1)² = 15
a: Ta có: \(\left(x+2\right)\left(x^2-2x+4\right)-x\left(x^2+2\right)=15\)
\(\Leftrightarrow x^3+8-x^3-2x=15\)
\(\Leftrightarrow2x=-7\)
hay \(x=-\dfrac{7}{2}\)
b: Ta có: \(\left(x-2\right)^3-\left(x-4\right)\left(x^2+4x+16\right)+6\left(x+1\right)^2=49\)
\(\Leftrightarrow x^3-6x^2+12x-8-x^3+64+6\left(x+1\right)^2=49\)
\(\Leftrightarrow-6x^2+12x+56+6x^2+12x+6=49\)
\(\Leftrightarrow24x=-13\)
hay \(x=-\dfrac{13}{24}\)
Đúng 0
Bình luận (0)
Bài 60 (trang 33 SGK Toán 9 Tập 1)
Cho biểu thức $B=\sqrt{16 x+16}-\sqrt{9 x+9}+\sqrt{4 x+4}+\sqrt{x+1}$ với $x \geq-1$.
a) Rút gọn biểu thức $B$;
b) Tìm $x$ sao cho $B$ có giá trị là $16$.
\(a,B=4\sqrt{x=1}-3\sqrt{x+1}+2\)\(\sqrt{x+1}+\sqrt{x+1}\)
\(=4\sqrt{x+1}\)
\(b,\)đưa về \(\sqrt{x+1}=4\Rightarrow x=15\)
a, Với \(x\ge-1\)
\(\Rightarrow B=4\sqrt{x+1}-3\sqrt{x+1}+2\sqrt{x+1}+\sqrt{x+1}\)
\(=4\sqrt{x+1}\)
b, Ta có B = 16 hay
\(4\sqrt{x+1}=16\Leftrightarrow\sqrt{x+1}=4\)bình phương 2 vế ta được
\(\Leftrightarrow x+1=16\Leftrightarrow x=15\)
a) B = 4√x+1 b) x = 15
Xem thêm câu trả lời
Biết 2/3x(x^2-16)=0 . Các số x tìm được là A.-1 B.0;16;-16 C.0;4 D.4;-4
Lời giải:
$\frac{2}{3}x(x^2-16)=0$
$\Leftrightarrow x=0$ hoặc $x^2-16=0$
$\Leftrightarrow x=0$ hoặc $(x-4)(x+4)=0$
$\Leftrightarrow x=0$ hoặc $x-4=0$ hoặc $x+4=0$
$\Leftrightarrow x=0$ hoặc $x=\pm 4$
Không có đáp án nào đúng.
Đúng 1
Bình luận (0)
1) Tìm x biết:
a)-(2x-16)-(x-8)=24
b)-3.(-x-4)-x=42-24
c)|2x-4|-16=-8
Tìm x:
a) (x²-16)(3x+2)=
b) 50% .x + ⅗(x-5) =
c) \(\dfrac{3}{4}+\dfrac{1}{4}:\:x\:=\:-\dfrac{1}{3}\)
Cho biểu thức
B = 16 x + 16 − 9 x + 9 + 4 x + 4 + x + 1
với x ≥ -1.
a) Rút gọn biểu thức B;
b) Tìm x sao cho B có giá trị là 16.
a) Rút gọn:
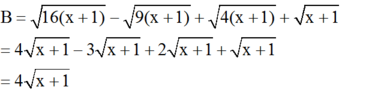
b) Để B = 16 thì:
⇔ x + 1 = 16 ⇔ x = 15 (thỏa mãn x ≥ -1)
Đúng 0
Bình luận (0)