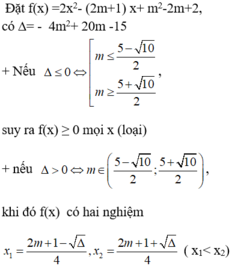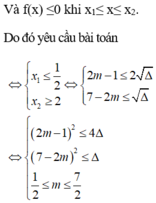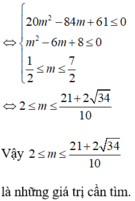Tìm m để :x^2 -2(m+1)x + m^2 +2m bé hơn hoặc bằng 0 có nghiệm đúng với mọi x thuộc [0;1]

Những câu hỏi liên quan
Cho f(x)=1/3(m-1)x³-mx²+(m+2)x-5. Tìm m để a)f'(x) lớn hơn hoặc bằng 0 với mọi x b)f'(x) nhỏ hơn hoặc bằng 0 với mọi x c)f'(x)=0 có 2 nghiệm cùng âm d)f'(x)=0 có nghiệm thỏa mãn x1+2x2=1
Cho 1/3(m-1)x³-(m-1)x²+(m-3)x+2. Tìm m để a)y'=0 có 2 nghiệm phân biệt cùng dương b)y'=0 có 2 nghiệm phân biệt trái dấu c)y'=0 có 2 nghiệm phân biệt|x1-x2|= căn 2 d)y' lớn hơn hoặc bằng 0 với mọi x e)y' nhỏ hơn hoặc bằng 0 với mọi x
Cho 1/3(m-1)x³-(m-1)x²+(m-3)x+2. Tìm m để a)y'=0 có 2 nghiệm phân biệt cùng dương b)y'=0 có 2 nghiệm phân biệt trái dấu c)y'=0 có 2 nghiệm phân biệt|x1-x2|= căn 2 d)y' lớn hơn hoặc bằng 0 với mọi x e)y' nhỏ hơn hoặc bằng 0 với mọi x
cho phương trình x^2-(2m-1)x +m^2-m =0 . tìm m để phương trình có 2 nghiệm phân biệt x1;x2 thoả mãn |x1 -2x| bé hơn hoặc bằng 5
\(\Delta=\left(2m-1\right)^2-4\left(m^2-m\right)=1>0\) ;\(\forall m\)
\(\Rightarrow\) Phương trình luôn có 2 nghiệm pb với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m-1\\x_1x_2=m^2-m\end{matrix}\right.\)
\(\left|x_1-x_2\right|\le5\)
\(\Leftrightarrow\left(x_1-x_2\right)^2\le25\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2\le25\)
\(\Leftrightarrow\left(2m-1\right)^2-4\left(m^2-m\right)\le25\)
\(\Leftrightarrow1\le25\) (luôn đúng)
Vậy bài toán thỏa mãn với mọi m
Đúng 0
Bình luận (0)
1. cho phương trình x^2-2(m-3)x-2m-100 tìm giá trị nhỏ nhất của biểu thức A x1^2 +x2^2-x1x2 2. cho phương trình x^2-(2m-1)x +m^2-m 0 . tìm m để phương trình có 2 nghiệm phân biệt x1;x2 thoả mãn |x1 -2x| bé hơn hoặc bằng 5 3. cho phương trình x^2 - (2m-1)x -2m -11 0 . tìm m để phương trình có 2 nghiệm phân biệt x1 ;x2 thoả mãn |x1 -x2| bé hơn hoặc bằng 44.hai ca nô cùng rời bến A đến bến B .ca nô thứ nhất mỗi giờ chạy nhanh hơn ca nô thứ hai 5km nên đến B sớm hơn ca nô thứ hai 30 phút .tí...
Đọc tiếp
1. cho phương trình x^2-2(m-3)x-2m-10=0 tìm giá trị nhỏ nhất của biểu thức A = x1^2 +x2^2-x1x2
2. cho phương trình x^2-(2m-1)x +m^2-m =0 . tìm m để phương trình có 2 nghiệm phân biệt x1;x2 thoả mãn |x1 -2x| bé hơn hoặc bằng 5
3. cho phương trình x^2 - (2m-1)x -2m -11 =0 . tìm m để phương trình có 2 nghiệm phân biệt x1 ;x2 thoả mãn |x1 -x2| bé hơn hoặc bằng 4
4.hai ca nô cùng rời bến A đến bến B .ca nô thứ nhất mỗi giờ chạy nhanh hơn ca nô thứ hai 5km nên đến B sớm hơn ca nô thứ hai 30 phút .tính vận tốc mỗi ca nô biết quãng đường AB dài 75 km
3:
\(\Delta=\left(2m-1\right)^2-4\left(-2m-11\right)\)
=4m^2-4m+1+8m+44
=4m^2+4m+45
=(2m+1)^2+44>=44>0
=>Phương trình luôn có hai nghiệm pb
|x1-x2|<=4
=>\(\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}< =4\)
=>\(\sqrt{\left(2m-1\right)^2-4\left(-2m-11\right)}< =4\)
=>\(\sqrt{4m^2-4m+1+8m+44}< =4\)
=>0<=4m^2+4m+45<=16
=>4m^2+4m+29<=0
=>(2m+1)^2+28<=0(vô lý)
Đúng 0
Bình luận (0)
Tìm m để bpt 2x2- (2m+1) x+ m2-2m+2≤ 0 nghiệm đúng với mọi
x
∈
1
2
;
2
A.
2
≤
m
≤
21
+
2
34
10
B.
m
≤...
Đọc tiếp
Tìm m để bpt 2x2- (2m+1) x+ m2-2m+2≤ 0 nghiệm đúng với mọi x ∈ 1 2 ; 2
A. 2 ≤ m ≤ 21 + 2 34 10
B. m ≤ 21 + 2 34 10
C. m ≥ 2
D. 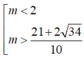
tìm m để phương trình x^2-(m+3)x+2m+2=0 có đúng 1 nghiệm thuộc (-∞;3]
\(x^2-\left(m+3\right)x+2m+2=0\Leftrightarrow\left(x-2\right)\left(x-m-1\right)=0\left(1\right)\)
\(\Delta=\left(m+3\right)^2-4\left(2m+2\right)=m^2+6m+9-8m-8=m^2-2m+1=\left(m-1\right)^2\ge0\left(\forall m\right)\)
\(\Rightarrow\left(1\right)\) \(luôn\) \(có\) \(nghiệm\) \(\forall m\)
\(\left(1\right)\Rightarrow\left[{}\begin{matrix}x=2\in(-\text{∞};3]\\x=m+1\end{matrix}\right.\)
\(\left(1\right)\) \(có\) \(đúng\) \(1\) \(nghiệm\) \(\in(-\text{∞};3]\) \(\Leftrightarrow\left[{}\begin{matrix}x=m+1=2\\x=m+1>3\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}m=1\\m>2\end{matrix}\right.\)
\(\Rightarrow\left\{1\right\}\cup\left(2;+\text{∞}\right)\)
\(\)
Đúng 1
Bình luận (0)
1. Tìm các giá trị của m để phương trình 3x2 - 4a + 2(m-1) = 0 có hai nghiệm phân biệt nhỏ hơn 2
2. Tìm các giá trị của m để phương trình x2 +mx -1 - 0 có ít nhất một nghiệm lớn hơn hoặc bằng 2
3. Cho phương trình mx2 - (2m-1)x +m+2 = 0 (5). Tìm hệ thức liên hệ giữa các nghiệm x1, x2 của (5) không phụ thuộc vào m
2.giải phương trình trên , ta được :
\(x_1=\frac{-m+\sqrt{m^2+4}}{2};x_2=\frac{-m-\sqrt{m^2+4}}{2}\)
Ta thấy x1 > x2 nên cần tìm m để x1 \(\ge\)2
Ta có : \(\frac{-m+\sqrt{m^2+4}}{2}\ge2\) \(\Leftrightarrow\sqrt{m^2+4}\ge m+4\)( 1 )
Nếu \(m\le-4\)thì ( 1 ) có VT > 0, VP < 0 nên ( 1 ) đúng
Nếu m > -4 thì ( 1 ) \(\Leftrightarrow m^2+4\ge m^2+8m+16\Leftrightarrow m\le\frac{-3}{2}\)
Ta được : \(-4< m\le\frac{-3}{2}\)
Tóm lại, giá trị phải tìm của m là \(m\le\frac{-3}{2}\)
Cho f(x)=\(-x^2+\left(2\sqrt{m}-1\right)x-m+\sqrt{m}\)
a)tìm m để f(x) >=0 vô nghiệm(lớn hơn = 0)
b)tìm m để f(x) >=0 với mọi x thuộc [1;2]
\(a=-1< 0;\Delta=\left(2\sqrt{m}-1\right)^2+4\left(\sqrt{m}-m\right)=4m-4\sqrt{m}+1+4\sqrt{m}-4m=1>0\)
a/ \(f\left(x\right)\ge0\) vô nghiệm \(\Leftrightarrow f\left(x\right)< 0,\forall x\in R\Leftrightarrow\left\{{}\begin{matrix}a=-1< 0\left(tm\right)\\\Delta< 0\left(voly\right)\end{matrix}\right.\)
Vậy ko tồn tại m để ....
b/ \(f\left(x\right)\ge0,\forall x\in\left[1;2\right]\)
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta>0\\\left[{}\begin{matrix}1< x_1< x_2\\x_1< x_2< 2\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}-1.f\left(1\right)>0\\\dfrac{x_1+x_2}{2}-1>0\end{matrix}\right.\\\left\{{}\begin{matrix}-1.f\left(2\right)>0\\\dfrac{x_1+x_2}{2}-2< 0\end{matrix}\right.\end{matrix}\right.\)
\(\left(1\right)\left\{{}\begin{matrix}-1+2\sqrt{m}-1-m+\sqrt{m}< 0\\\sqrt{m}-\dfrac{1}{2}-1>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m-3\sqrt{m}+2>0\\\sqrt{m}>\dfrac{3}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}0< m< 1\\m>2\end{matrix}\right.\\m>\dfrac{9}{4}\end{matrix}\right.\Leftrightarrow m>\dfrac{9}{4}\)
\(\left(2\right)\left\{{}\begin{matrix}-4+4\sqrt{m}-2-m+\sqrt{m}< 0\\\sqrt{m}-\dfrac{1}{2}-2< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m-5\sqrt{m}+6>0\\\sqrt{m}< \dfrac{5}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}0< m< 2\\m>3\end{matrix}\right.\\0\le m< \dfrac{25}{4}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}0< m< 2\\3< m< \dfrac{25}{4}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}m>\dfrac{9}{4}\\0< m< 2\\3< m< \dfrac{25}{4}\end{matrix}\right.\)
Đúng 0
Bình luận (0)