Vẽ đoạn AB=6cm
Vẽ đường tròn[A;3cm]
Vẽ đường tròn [B;4cm]
Đường tròn [A;3cm] cắt [B;4cm] tại C và D
Tính chu vi tam giác ABC và tam giác ADB
Những câu hỏi liên quan
Vẽ tam giác ABC có B=120 độ , AB=3cm bc=6cm
Vẽ đường cao AH và trung tuyết AM và tam giác ABC
Cho đoạn thẳng AB. Vẽ M là trung điểm của đoạn thẳng AB. Vẽ đường tròn (M;2,5cm). a, tính MA b, điểm A và B có thuộc đường tròn không? Vì sao? c, Vẽ (A;2cm) đường tròn (A;2cm ) cắt đường thẳng AB tại Q. So sánh AQ và BM Nhớ vẽ hình
a) MA=2,5cm
b) A và B có thuộc đường tròn
Đúng 0
Bình luận (0)
cho đoạn thẳng Ab dài 4cm . Vẽ đường tròn tâm a 3cm cắt đoạn thẳng Ab tại K ,vẽ đường tròn tâm B 2cm cắt đoạn thẳng tai I: a) tính KA và BI
Tự vẽ hình đi :)
Vì (A; 3cm) cắt đoạn thẳng Ab tại K
=> K thuộc (A; 3cm)
=> KA = 3cm
Vì (b; 2cm) cắt đoạn thẳng Ab tại I
=> I thuộc (B; 2cm)
=> IB = 2cm
Đúng 0
Bình luận (0)
Vẽ hình liên tiếp theo các cách diễn đạt sau:a. Vẽ đoạn thẳng AB2cm. Vẽ đường tròn (C1) tâm A , bán kính ABb. Vẽ đường tròn (C2) tâm B bán kính AB. Gọi các giao điểm của đường tròn này với đường tròn (C1) là C và G.c. Vẽ đường tròn (C3) tâm C, bán kính AC. Gọi giao điểm mới của đường tròn này với đường tròn (C1) là Dd. Vẽ đường tròn (C4) tâm D bán kính AD. Gọi giao điểm mới của đường tròn này với đường tròn (C1) là Ee. Vẽ đường tròn (C5) tâm E bán kính AE. Gọi giao điểm mới của đường tròn này...
Đọc tiếp
Vẽ hình liên tiếp theo các cách diễn đạt sau:
a. Vẽ đoạn thẳng AB=2cm. Vẽ đường tròn (C1) tâm A , bán kính AB
b. Vẽ đường tròn (C2) tâm B bán kính AB. Gọi các giao điểm của đường tròn này với đường tròn (C1) là C và G.
c. Vẽ đường tròn (C3) tâm C, bán kính AC. Gọi giao điểm mới của đường tròn này với đường tròn (C1) là D
d. Vẽ đường tròn (C4) tâm D bán kính AD. Gọi giao điểm mới của đường tròn này với đường tròn (C1) là E
e. Vẽ đường tròn (C5) tâm E bán kính AE. Gọi giao điểm mới của đường tròn này với đường tròn (C1) là F
f. Vẽ đường tròn (C6) tâm F bán kính AF
g. Vẽ đường tròn (C7) tâm G bán kính AG
Sau khi vẽ như trên hãy so sánh các đoạn thẳng AB, BC, CD, DE, EF, FG, GB
Sau khi vẽ ta được hình như sau:
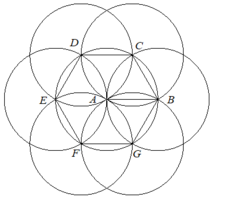
Khi đó, các đoạn thẳng A B = B C = C D = D E = E F = F G = G B (vì cùng bằng bán kính).
Đúng 0
Bình luận (0)
Vẽ đoạn thẳng AB=4cm,vẽ đường tròn tâm A bán kính 3cm,vẽ đường tròn tâm B bán kính 2cm cắt nhau tại C,D.
Đường tròn tâm A cắt AB tại K.Đường tròn tâm B cắt AB tại I .
a)Tính các đoạn thẳng CA,CB
b)Chứng tỏ I là trung điểm AB
c)Tính Ik
a)CA=3cm, CB=2cm. Vì chúng đều là bán kính của từng hình tròn.
b)Bán kính đường tròn tâm B là 2cm => IB=2cm
Mà AB=IA+IB=4cm
=>IA=IB=2cm
=> I trung điểm AB.
c)IK+KB=IB=2cm
AK+KB=AB=4cm
=>3+KB=4
=> KB=1cm
=> IK=1cm
Đúng 0
Bình luận (0)
Vẽ đoạn thẳng AB bằng 3cm.
Vẽ đường tròn tâm A bán kính 2cm.
Vẽ đường tròn tâm B bán kính 2cm.
Đặt tên giao điểm của hai đường tròn là C, D.
Vẽ đoạn thẳng CD.
Đặt tên giao điểm của AB và CD là I.
Đo IA và IB.
Vẽ đoạn thẳng ab = 5cm vẽ đường tròn. vẽ đường tròn (A,4cm) và (B;2cm),chúng cắt nhau tại C và D.
a)tính độ dài đoạn thẳng AC và BC
b)gọi K là trung điểm của đoạn thẳng AB . chứng tỏ điểm K nằm bên trong đường tròn (A,4cm)
Cho hai điểm A, B cách nhau 5cm. Vẽ đường tròn (A; 1,5cm) và đường tròn (B; 2,5cm). Đường tròn (A; 1,5cm) cắt đoạn AB tại C, đường tròn (B; 2cm) cắt đoạn AB tại D. Khẳng định nào sau đây sai? A. Điểm C nằm trong đường tròn (B; 2,5cm). B. Điểm C nằm giữa A và D C. Điểm D nằm ngoài đường tròn (A; 1,5cm) D. Điểm D là trung điểm của AB
Đọc tiếp
Cho hai điểm A, B cách nhau 5cm. Vẽ đường tròn (A; 1,5cm) và đường tròn (B; 2,5cm). Đường tròn (A; 1,5cm) cắt đoạn AB tại C, đường tròn (B; 2cm) cắt đoạn AB tại D. Khẳng định nào sau đây sai?
A. Điểm C nằm trong đường tròn (B; 2,5cm).
B. Điểm C nằm giữa A và D
C. Điểm D nằm ngoài đường tròn (A; 1,5cm)
D. Điểm D là trung điểm của AB
Đáp án là A
C ∈ ( A ; 1,5 c m ) ⇒ A C = 1,5 c m ⇒ B C = A B − A C = 5 − 1,5 = 3,5 c m
B C > B D ⇒ C nằm ngoài C ( B ; 2,5 c m ) nên A sai.
D ∈ ( B ; 2,5 c m ) ⇒ B D = 2,5 c m ⇒ A D = A B − B D = 5 − 2,5 = 2,5 c m
Do đó AD = BD nên D là trung điểm AB nên D đúng.
Vì AD > AC nên C nằm giữa A và D và D nằm ngoài (A; 1,5cm).
Nên B và C đúng.
Đúng 0
Bình luận (0)
a) Vẽ tam giác ABC. Vẽ các đường trung trực của các đoạn thẳng AB, BC, CA
b) Vẽ đường tròn tâm O bán kính R = 3(cm). Lấy 3 điểm A, B, C phân biệt bất kì trên đường tròn. Vẽ các dây AB, BC, CA. Vẽ các đường trung trực của đoạn thẳng AB, BC, CA
Vẽ hình liên tiếp theo cách diễn đạt sauVẽ đoạn thẳng AB 2cm. Vẽ đường tròn (c1) tâm A, bán kính AB.Vẽ đường tròn (c2) tâm B, bán kính AB. Gọi các giao điểm của đường tròn này với đường tròn (c1) là C và G.Vẽ đường tròn (c3) tâm C, bán kính AC. Goi giao điểm mới củađường tròn này với đường tròn (c1) là D.Vẽ đường tròn (c4) tâm D, bán kính AD. Gọi giao điểm mới của đường tròn này với đường tròn (c1) là E.Vẽ đường tròn (c5) tâm E, bán kính AE. Gọi giao điểm mới của đường tròn này với đường tròn (...
Đọc tiếp
Vẽ hình liên tiếp theo cách diễn đạt sau
Vẽ đoạn thẳng AB = 2cm. Vẽ đường tròn (c1) tâm A, bán kính AB.
Vẽ đường tròn (c2) tâm B, bán kính AB. Gọi các giao điểm của đường tròn này với đường tròn (c1) là C và G.
Vẽ đường tròn (c3) tâm C, bán kính AC. Goi giao điểm mới củađường tròn này với đường tròn (c1) là D.
Vẽ đường tròn (c4) tâm D, bán kính AD. Gọi giao điểm mới của đường tròn này với đường tròn (c1) là E.
Vẽ đường tròn (c5) tâm E, bán kính AE. Gọi giao điểm mới của đường tròn này với đường tròn (c1) là F
Vẽ đường tròn (c6) tâm F, bán kính AF.
Vẽ đường tròn (c7) tâm G, bán kính AG.
Sau khi vẽ như trên hãy so sánh các đoạn thẳng: AB, BC, CD, DE, EF, FG, GB
Sau khi vẽ ta được hình bs.17
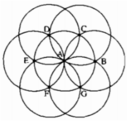
Khi đó, các đoạn thẳng: AB, BC, CD, EF, FG, GB bằng nhau (vì cùng bằng bán kính).
Đúng 0
Bình luận (0)