Ta thấy : \(\text{Ư}\left(36\right)=\left\{\pm1;\pm2;\pm3;\pm4;\pm6;\pm12;\pm18;\pm36\right\}\)

Vì \(\frac{a}{b}\)tối giản và a.b = 36 nên được: \(\frac{1}{36};\frac{-1}{-36}\)

Vậy \(\frac{a}{b}=\left\{\frac{1}{36};\frac{-1}{-36}\right\}\)

#Chúc em học tốt

ko có j âu em

Ta thấy: \(Ư\left(36\right)=\left\{1\pm;\pm2;\pm3;\pm4;\pm6;\pm9;\pm12;\pm18;\pm36\right\}\)

Vì tối giản nên viết đc: \(\frac{1}{36};\frac{-1}{-36}\)

Các p/s khác viết đc nhưng k tối giản hoặc tối giản nhưng ab k = 36

Hội con 🐄 chúc bạn học tốt!!! 

ta có U( 36) = { 1;-1;2;-2;3;-3;4;-4;6;-6;9;-9;12;-12;36;-36}

mà a phần b tối giản ; ab = 36

=> a/b = 1/ 36 = -1/36

Ta có \(Ư\left(36\right)=\left\{\text{ ±}1;\text{ ±}2;\text{ ±}3;\text{ ±}4;\text{ ±}6;\text{ ±}9;\text{ ±}12;\text{ ±}18;\text{ ±}36\right\}\)

Ta viết được \(\text{ ±}\dfrac{1}{36}\)

Đặt x + 1 t = t , t ≥ 2  khi đó phương trình trở thành 2 t 2 − 3 t − 5 m − 3 = 0    ( * )

Phương trình  2 x 2 + 1 x 2 - 3 x + 1 x - 5 m + 1 = 0 có nghiệm khi và chỉ khi phương trình (*) có nghiệm t thỏa mãn  t ≥ 2

Số nghiệm của phương trình (*) bằng số giao điểm của parabol (P): y = 2 t 2 − 3 t − 3 và đường thẳng d : y = 5 m

Xét parabol  P : y = 2 t 2 - 3 t - 3 ta có bảng biến thiên như sau:

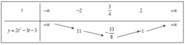
Từ bảng biến thiên ta có phương trình (*) có nghiệm  t ∈ ( - ∞ ; - 2 ] ∪ [ 2 ; + ∞ )  khi và chỉ khi  5 m ≥ - 1  hoặc  5 m ≥ 11

Vậy khi m ∈ − 1 5 ; + ∞ thì phương trình có nghiệm ⇒ a = 1 b = 5 ⇒ T = 5

Đáp án cần chọn là: B

Điều kiện xác định: x ≠ 0 .

Đặt  t = x + 1 x ⇒ t 2 − 2 = x 2 + 1 x 2 ≥ 2 ⇒ t ≥ 2 ⇔ t ≥ 2 t ≤ − 2

Phương trình đã cho trở thành  2 t 2 − 2 − 3 t − 2 m + 1 = 0

⇔ 2 t 2 − 3 t − 2 m − 3 = 0 ⇔ 2 t 2 − 3 t − 3 = 2 m      ( 1 )

Xét hàm số y = f ( t ) = 2 t 2 − 3 t − 3 có bảng biến thiên:

(1) Có nghiệm t thỏa mãn t ≥ 2 t ≤ − 2     k h i    2 m ≥ − 1 2 m ≥ 11 ⇔ m ≥ − 1 2 ⇒ S = − 1 2 ; + ∞

Vậy T = 3

Đáp án cần chọn là: D

nhìn rối quá ạ :v tách ra từng bài một hộ tớ

Bài 16: 

1/36; 36/1; 4/9; 9/4

Bài 17:

a: a/b=3/4=45/60

b: a/b=3/5=90/150

#)Giải :

Xét ab = 100

=> ab = { 25;4 } ; { 1;100 } 

Với các cặp số trên, ta viết được các phân số : \(\frac{25}{4};\frac{4}{25};\frac{1}{100};\)