Chứng minh rằng phương trình sau vô nghiệm:
x4 - x3 + 2x2 - x + 1 = 0
Chứng tỏ rằng các phương trình sau đây vô nghiệm:
a. 2(x+1)=3+2x2(x+1)=3+2x
b. 2(1−1,5x)+3x=02(1−1,5x)+3x=0
c. |x|=−1
a. Ta có: 2(x+1)=3+2x2(x+1)=3+2x
⇔2x+2=3+2x⇔0x=1⇔2x+2=3+2x⇔0x=1
Vậy phương trình vô nghiệm.
b. Ta có: 2(1−1,5x)+3x=02(1−1,5x)+3x=0
⇔2−3x+3x=0⇔2+0x=0⇔2−3x+3x=0⇔2+0x=0
Vậy phương trình vô nghiệm.
c. Vì |x|≥0|x|≥0 nên phương trình |x|=−1|x|=−1 vô nghiệm.
cứ đưa vào máy vinacal... ra nghiệm ảo thì là vô nghiệm.. hé hé hé :))))
Chứng minh rằng phương trình x 3 + x - 1 = 0 có nghiệm duy nhất x 0 thỏa mãn 0 < x 0 < 1 2
- Xét hàm số f ( x ) = x 3 + x - 1 , ta có f(0) = -1 và f(1) = 1 nên: f(0).f(1) < 0.
- Mặt khác: f ( x ) = x 3 + x - 1 là hàm đa thức nên liên tục trên [0;1].

- Suy ra f ( x ) = x 3 + x - 1 đồng biến trên R nên phương trình x 3 + x - 1 = 0 có nghiệm duy nhất x 0 ∈ ( 0 ; 1 ) .
- Theo bất đẳng thức Côsi:
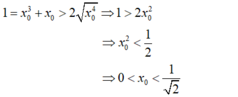
Chứng minh rằng phương trình x3 -3x2-1=0 có nghiệm x thuộc (3,4) và x > 1+\(\sqrt[5]{36}\)
Em 2k8 nên e k chắc :((
Đặt f(x) = x^3 - 3x^2 - 1 = 0 => f(x) liên tục trên (3;4)
x = 3 => f(3) = -1 ; x = 4 => f(4) = 15
=> f(3) . f(4) = -15 < 0 => tồn tại no x thuộc (3;4) để f(x) = 0 ( đpcm )
Chứng minh rằng phương trình sau vô nghiệm
x4 + x3 + x2 + x + 1 = 0
GHÉP THÀNH 2 ĐA THỨC BẬC HAI
(X^4 + 2*X^3/2+x^2/4)+(X^2/4+2*X/2+1)+X^2/2
(X^2+x/2)^2+(X/2+1)^2+X^2/2
ĐÚNG THÌ K
- Ta có: \(x^4+x^3+x^2+x+1=0\)( * )
- Nhân \(x-1\)vào cả hai vế của phương trình ( * ), ta có:
\(\left(x^4+x^3+x^2+x+1\right).\left(x-1\right)=0.\left(x-1\right)\)
\(\Leftrightarrow x^5+x^4+x^3+x^2+x-x^4-x^3-x^2-x-1=0.\left(x-1\right)\)
\(\Leftrightarrow x^5+\left(x^4-x^4\right)+\left(x^3-x^3\right)+\left(x^2-x^2\right)+\left(x-x\right)-1=0.\left(x-1\right)\)
\(\Leftrightarrow\frac{x^5-1}{x-1}=0\)( ** )
\(\Leftrightarrow x^5-1=0\)
\(\Leftrightarrow x^5=1\)
\(\Leftrightarrow x=1\)
- Thay \(x=1\)vào phương trình ( ** ), ta có:
\(\frac{1^5-1}{1-1}=\frac{1-1}{0}\)( vô nghiệm )
Vậy phương trình \(x^4+x^3+x^2+x+1=0\)vô nghiệm ( ĐPCM )
cảm ơn hai bạn nhiều
Cho phương trình :x^2-2(2m-1)x+m(m-1)=0
Gọi x1 và x2 là nghiệm của phương trình (x1<x2)
Chứng minh rằng (x1)^2-2x2+3>0
Cho phương trình: x² - mx + m - 1 = 0(x là ẩn) a) Chứng minh rằng phương trình luôn có nghiệm với mọi giá trị của m b) Tìm giá trị của m để phương trình có 2 nghiệm x1, x2 thoả mãn: x1 - 2x2 = 1
Bài 1: Giải phương trình:
a) ( x+1)2 (x+2) + ( x – 1)2 ( x- 2) = 12
b) x4 + 3x3 + 4x2 + 3x + 1 = 0
c) x5 – x4 + 3x3 + 3x2 –x + 1 = 0
Bài 2: Chứng minh rằng các phương trình sau vô nghiệm
a) x4 – x3 + 2x2 – x + 1 = 0
b) x4 + x3 + x2 + x + 1 = 0
c) x4 – 2x3 +4x2 – 3x +2 = 0
d) x6+ x5+ x4 + x3 + x2 + x + 1 = 0
1.
a/ \(\Leftrightarrow\left(x+1\right)\left(x^2+3x+2\right)+\left(x-1\right)\left(x^2-3x+2\right)-12=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2+2\right)+3x\left(x+1\right)-3x\left(x-1\right)+\left(x-1\right)\left(x^2+2\right)-12=0\)
\(\Leftrightarrow2x\left(x^2+2\right)+6x^2-12=0\)
\(\Leftrightarrow x^3+3x^2+2x-6=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2+4x+6\right)=0\Rightarrow x=1\)
b/ Nhận thấy \(x=0\) ko phải nghiệm, chia 2 vế cho \(x^2\)
\(x^2+\frac{1}{x^2}+3\left(x+\frac{1}{x}\right)+4=0\)
Đặt \(x+\frac{1}{x}=t\Rightarrow x^2+\frac{1}{x^2}=t^2-2\)
\(t^2-2+3t+4=0\Rightarrow t^2+3t+2=0\Rightarrow\left[{}\begin{matrix}t=-1\\t=-2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x+\frac{1}{x}=-1\\x+\frac{1}{x}=-2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x^2+x+1=0\left(vn\right)\\x^2+2x+1=0\end{matrix}\right.\) \(\Rightarrow x=-1\)
1c/
\(\Leftrightarrow x^5+x^4-2x^4-2x^3+5x^3+5x^2-2x^2-2x+x+1=0\)
\(\Leftrightarrow x^4\left(x+1\right)-2x^3\left(x+1\right)+5x^2\left(x+1\right)-2x\left(x+1\right)+x+1=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^4-2x^3+5x^2-2x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x^4-2x^3+5x^2-2x+1=0\left(1\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow x^4-2x^3+x^2+x^2-2x+1+3x^2=0\)
\(\Leftrightarrow\left(x^2-x\right)^2+\left(x-1\right)^2+3x^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2-x=0\\x-1=0\\x=0\end{matrix}\right.\) \(\Rightarrow\) không tồn tại x thỏa mãn
Vậy pt có nghiệm duy nhất \(x=-1\)
2.
a. \(x^4-x^3+x^2+x^2-x+1=0\)
\(\Leftrightarrow x^2\left(x^2-x+1\right)+x^2-x+1=0\)
\(\Leftrightarrow\left(x^2+1\right)\left(x^2-x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2+1=0\left(vn\right)\\x^2-x+1=0\Leftrightarrow\left(x-\frac{1}{2}\right)^2+\frac{3}{4}=0\left(vn\right)\end{matrix}\right.\)
Vậy pt vô nghiệm
b.
\(x^4+x^3+x^2+x+1=0\)
\(\Leftrightarrow x\left(x^3+1\right)+x^3+1+x^2=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^3+1\right)+x^2=0\)
\(\Leftrightarrow\left(x+1\right)^2\left(x^2-x+1\right)+x^2=0\)
Mà \(\left\{{}\begin{matrix}\left(x+1\right)^2\left(x^2-x+1\right)\ge0\\x^2\ge0\end{matrix}\right.\)
Nên dấu "=" xảy ra khi và chỉ khi: \(\left\{{}\begin{matrix}x+1=0\\x=0\end{matrix}\right.\) ko tồn tại x thỏa mãn
Gọi n là số các giá trị của tham số m để bất phương trình ( 2 m - 4 ) ( x 3 + 2 x 2 ) + ( m 2 - 3 m + 2 ) - ( m 3 – m 2 - 2 m ) ( x + 2 ) < 0 vô nghiệm. Giá trị của n bằng
A. 5
B. 1
C. 4
D. 2
Chứng minh rằng phương trình x 3 + 6 x + 1 - 2 = 0 có nghiệm dương