Cho ba chữ số a b c thỏa mãn ba điều kiện sau; a<b<c
11<a<15 ; 12<c<15 khi đó a+b+c bằng
giải ra đầy đủ được 1 tick
Những câu hỏi liên quan
cho ba chữ số a,b,c thỏa mãn điều kiện sau ; a<b <c, 28<a<28;15<c<31. Khi đó a + b -c =......
bài 3dùng cả ba chữ số 2;4;5, hãy ghép thành các số tự nhiên có ba chữ số thỏa mãn một trong các điều kiện sau1)số đó chia hết cho 22)số đó chia hết cho 5b)dùng cả ba chữ số 5;6;7, hãy ghép thành các số tự nhiên có ba chữ số thỏa mãn một trong các điều kiện sau1)lớn nhất và chia hết cho 22)số đó nhỏ nhất và chia hết cho 5c)dùng cả ba chữ số 2;4;5, hãy ghép thành các số tự nhiên có ba chữ số thỏa mãn một trong các điều kiện sau1)lớn nhất và chia hết cho 52)số đó nhỏ nhất và chia hết cho 2
Đọc tiếp
bài 3
dùng cả ba chữ số 2;4;5, hãy ghép thành các số tự nhiên có ba chữ số thỏa mãn một trong các điều kiện sau
1)số đó chia hết cho 2
2)số đó chia hết cho 5
b)dùng cả ba chữ số 5;6;7, hãy ghép thành các số tự nhiên có ba chữ số thỏa mãn một trong các điều kiện sau
1)lớn nhất và chia hết cho 2
2)số đó nhỏ nhất và chia hết cho 5
c)dùng cả ba chữ số 2;4;5, hãy ghép thành các số tự nhiên có ba chữ số thỏa mãn một trong các điều kiện sau
1)lớn nhất và chia hết cho 5
2)số đó nhỏ nhất và chia hết cho 2
a) 1) 254;524;542;452
2) 245;425
b) 1) 756
2) 675
c) 1) 425
2) 254
Đúng 0
Bình luận (0)
a)
1) số 452; 542; 254; 524 chia hết cho 2
2) số 245; 425 chia hết cho 5
b)
1) 756
2) 675
c)
1) 425
2) 254
học tốt!!!
Đúng 0
Bình luận (0)
cho ba số a,b,c thỏa mãn điều kiện sau a<b lớn hơn hoặc bằng <c
Cho ba số a, b, c thỏa mãn ba điều kiện sau: a < b < c; 11 < a < 15; 12 < c < 15. Khi đó a + b + c =
11<a<15
<=> a\(\in\left\{12;13;14\right\}\)
12<c<15
<=>c\(\in\left\{13;14\right\}\)
Mà a<b<c
<=>
a=12;b=13;c=14
Khi đó a+b+c=12+13+14=39
Đúng 0
Bình luận (0)
Tìm a, b, c là các chữ số thỏa mãn điều kiện: ba x 7 = caa
Tìm ba số tự nhiên a, b, c. Biết rằng chúng thỏa mãn đồng thời ba điều kiện sau: a < b < c ; 91 ≤ a ≤ 93 ; 91 < c < 94 .
Tìm ba số tự nhiên a;b;c biết rằng chúng thỏa mãn đồng thời ba điều kiện sau: a<b<c; 91≤a≤93; 91<c<94
Từ điều kiện 91≤a≤93 và a ∈ ¥ ta suy ra: a ∈ {91;92;93}
Từ điều kiện 91<c<94 và c ∈ ¥ ta suy ra: c ∈ {92;93}
Mặt khác, a<b<c (b là số tự nhiên) nên a = 91; b = 92; c = 93
Đúng 0
Bình luận (0)
cho ba số a,b,c thỏa mãn ba điều kiện sau : a < b < hoặc = c ; 28 < a < 38 ; 15 < c < 31.tính a+b-c
cách làm
Cho a;b;c là ba số thực dương,
a
1
và thỏa mãn
log
2
a
b
c
+
log
a
b
3
c
3
+
b
c...
Đọc tiếp
Cho a;b;c là ba số thực dương, a > 1 và thỏa mãn log 2 a b c + log a b 3 c 3 + b c 4 2 + 4 + 4 - c 2 = 0 . Số bộ a;b;c thỏa mãn điều kiện đã cho là:
A. 0
B. 1
C. 2
D. vô số
Ta có:
Dấu “=” xảy ra khi và chỉ khi
Vậy số bộ a,b,c thỏa mãn điều kiện đã cho là 1.
Chọn B.
Đúng 0
Bình luận (0)
Cho số a và ba số b, c, d khác a và thỏa mãn điều kiện c + d 2b. Giải phương trình
x
a
-
b
a
-
c
-
2
x
a
-
b...
Đọc tiếp
Cho số a và ba số b, c, d khác a và thỏa mãn điều kiện c + d = 2b. Giải phương trình x a - b a - c - 2 x a - b a - d + 3 x a - c a - d = 4 a a - c a - d
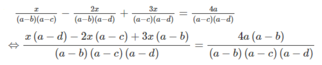
⇔ x(a − d) − 2x(a − c) + 3x(a − b) = 4a(a − b)
⇔ x(a − d − 2a + 2c + 3a − 3b) = 4a(a − b)
⇔ x(2a − 3b + 2c − d) = 4a(a − b)
Theo giả thiết, b + d = 2c nên 2a – 3b + 2c – d = 2a – 2b = 2 (a – b ).
Do đó phương trình đã cho tương đương với phương trình 2(a − b)x = 4a(a − b)
Để ý rằng a – b ≠ 0, ta thấy ngay phương trình cuối có nghiệm duy nhất x = 2a.
Vậy phương trình đã cho cũng có nghiệm duy nhất x = 2a.
Đúng 0
Bình luận (0)