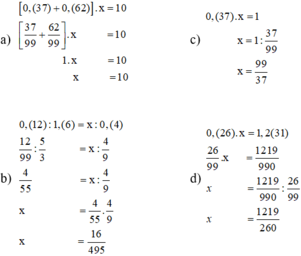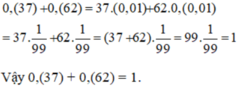0,(37) + 0,(62) = ......

Những câu hỏi liên quan
Chứng tỏ rằng:
a) 0,(37) + 0,(62) = 1
b) 0,(33) x 3 = 1
* 0,(37) = 0 phẩy chu kỳ 37
a) 0,(37)+0,(62) = 1
Có 0.(37)=\(\frac{37}{99}\)và 0.(62) = \(\frac{62}{99}\)
\(\frac{37}{99}\)+ \(\frac{62}{99}\)= 1
\(\Rightarrow0,\left(37\right)+0.\left(62\right)=1\)
b)\(0,\left(37\right)\times3=1\)
Có: \(0,\left(37\right)=\frac{37}{99}\)
\(\frac{37}{99}\times3=1\)
\(\Rightarrow0\left(37\right)\times3=1\)
Đúng 0
Bình luận (0)
0,(37) +0,(62)=?
Tìm x, biết:a)
0
,
(
37
)
+
0
,
(
62
)
.
x
10
b)
0
,
(
12
)
:
1
,
(
6
)
x
:
0
,
(
4
)...
Đọc tiếp
Tìm x, biết:
a) 0 , ( 37 ) + 0 , ( 62 ) . x = 10
b) 0 , ( 12 ) : 1 , ( 6 ) = x : 0 , ( 4 )
c) 0 , ( 37 ) . x = 1
d) 0 , ( 26 ) . x = 1 , 2 ( 31 )
Chứng tỏ rằng: 0,(37) + 0,(62) =1
(0,(37)+0,(62))xX=10
[0,(37)+0,(62)]*x=10
Bài làm:
Ta có: \(\left[0,\left(37\right)+0,\left(62\right)\right].x=10\)
\(\Leftrightarrow\left(\frac{37}{99}+\frac{62}{99}\right).x=10\)
\(\Leftrightarrow1.x=10\)
\(\Rightarrow x=10\)
\(\left[0,\left(37\right)+0,\left(62\right)\right]\cdot x=10\)
=> \(\left[\frac{37}{99}+\frac{62}{99}\right]\cdot x=10\)
=> \(1\cdot x=10\)
=> x = 10
Chứng tỏ rằng : 0, ( 37 ) + 0, ( 62 ) =1
0,(37)+0,(62)=37/99+62/99=99/99=1
Đúng 0
Bình luận (0)
tim x biet [0,(37)+0,(62)]x=10?
CTR: a) 0,(37)+0,(62)=1
tìm các số hữu tỉ a và b biết rằng hiệu a-b bằng thương a:b và bằng hai lần tổng a +b
Đúng 0
Bình luận (0)
\(0,\left(37\right)+0,\left(62\right)=\frac{37}{99}+\frac{62}{99}=\frac{99}{99}=1\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời