`|5x| = - 3x + 2`

Nếu `5x>=0<=> x>=0` thì phương trình trên trở thành :

`5x =-3x+2`

`<=> 5x +3x=2`

`<=> 8x=2`

`<=> x= 2/8=1/4` ( thỏa mãn )

Nếu `5x<0<=>x<0` thì phương trình trên trở thành :

`-5x = -3x+2`

`<=>-5x+3x=2`

`<=> 2x=2`

`<=>x=1` ( không thỏa mãn ) 

Vậy pt đã cho có nghiệm `x=1/4`

__

`6x-2<5x+3`

`<=> 6x-5x<3+2`

`<=>x<5`

Vậy bpt đã cho có tập nghiệm `x<5`

Ta có: -4x – 2 > -5x + 6 ⇔ -4x + 5x > 6 + 2 ⇔ x > 8

Vậy tập nghiệm của bất phương trình là: {x|x > 8}

Bài 1: 

a: \(\Leftrightarrow x^2-5x+6< =0\)

=>(x-2)(x-3)<=0

=>2<=x<=3

b: \(\Leftrightarrow\left(x-6\right)^2< =0\)

=>x=6

c: \(\Leftrightarrow x^2-2x+1>=0\)

\(\Leftrightarrow\left(x-1\right)^2>=0\)

hay \(x\in R\)

\(\frac{x^2\left(x-1\right)\left(x+1\right)}{\left(>0\right)}\le0\Rightarrow\left(x-1\right)\left(x+1\right)\le0\Rightarrow-1\le x\le1\)

x=0 đúng

a:=>3x=15

=>x=5

b: =>8-11x<52

=>-11x<44

=>x>-4

c: \(VT=\left(\dfrac{x^2-\left(x-6\right)^2}{x\left(x+6\right)\left(x-6\right)}\right)\cdot\dfrac{x\left(x+6\right)}{2x-6}+\dfrac{x}{6-x}\)

\(=\dfrac{12x-36}{2x-6}\cdot\dfrac{1}{x-6}-\dfrac{x}{x-6}=\dfrac{6}{x-6}-\dfrac{x}{x-6}=-1\)

\(f\left(x\right)=\dfrac{\left(3x-4\right)\left(2x-3\right)}{\left(x^2-5x+6\right)\left(5-x\right)}>0\)

\(\Leftrightarrow\dfrac{\left(3x-4\right)\left(2x-3\right)}{\left(x-2\right)\left(x-3\right)\left(5-x\right)}>0\)

Bảng xét dấu:

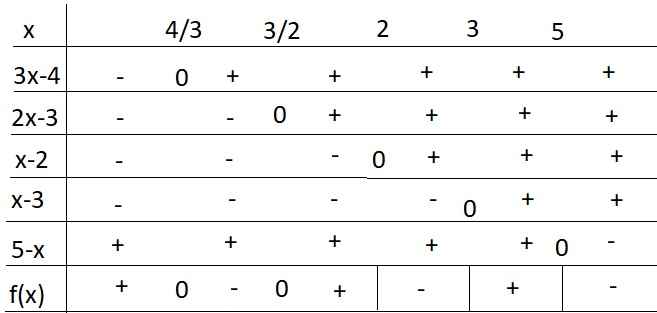
Từ bảng xét dấu ta thấy nghiệm của BPT là: \(\left[{}\begin{matrix}x< 5\\\dfrac{3}{2}< x< 2\\3< x< 5\end{matrix}\right.\)