CHo f(x) + 2f(\(\frac{1}{x}\)) =1
Tính f(2)
Cho f(x) thỏa mãn f(1)=1,f(2)=3,f(n)+f(x+2)=2f(n+1) Tính f(1)+f(2)+...+f(2019)
Cho hàm số f(x) xác định với mọi x thuộc R. Biết rằng với mọi x, ta đều có:\(f\left(x\right)+2f\left(\frac{1}{x}\right)=x^2.\)Tính \(f\left(\frac{1}{3}\right)\)
\(f\left(\frac{1}{3}\right)+2f\left(\frac{1}{\frac{1}{3}}\right)=\left(\frac{1}{3}\right)^2\Rightarrow f\left(\frac{1}{3}\right)+2f\left(3\right)=\frac{1}{9}\)(1)
\(f\left(3\right)+2f\left(\frac{1}{3}\right)=3^2\Rightarrow2f\left(3\right)+4f\left(\frac{1}{3}\right)=18\)(2)
Từ (1) và (2) \(\Rightarrow2f\left(3\right)+4f\left(\frac{1}{3}\right)-f\left(\frac{1}{3}\right)-2f\left(3\right)=18-\frac{1}{9}\)
\(\Rightarrow3f\left(\frac{1}{3}\right)=\frac{161}{9}\Rightarrow f\left(\frac{1}{3}\right)=\frac{161}{27}\)
Bài 1:cho hàm số f(x) xác định với mọi x thuộc R .Biết rằng với mọi x khác 0 ta đều có
\(f\left(x\right)+2f\left(\frac{1}{x}\right)=x^2\) .Tính f(2)
Bài 2:Tính tổng T=\(\frac{2}{2^1}+\frac{3}{2^2}+\frac{4}{2^3}+...+\frac{2015}{2^{2014}}\).Hãy so sánh T với 3
Cho các hàm số f(x) xác định với mọi x. Biết f(x) +2f(\(\frac{1}{x}\))=2x. Tính f(3)
\(f\left(3\right)+2f\left(\frac{1}{3}\right)=2.3=6\)=>\(2f\left(\frac{1}{3}\right)=6-f\left(3\right)\Leftrightarrow f\left(\frac{1}{3}\right)=3-\frac{f\left(3\right)}{2}\)
\(f\left(\frac{1}{3}\right)+2f\left(3\right)=2.\frac{1}{3}=\frac{2}{3}\)=> \(3-\frac{f\left(3\right)}{2}+2f\left(3\right)=\frac{2}{3}\Leftrightarrow\frac{3}{2}f\left(3\right)=\frac{2}{3}-3=-\frac{7}{3}\)
\(f\left(3\right)=-\frac{14}{9}\)
Giúp mình với :
Cho y=f(x)= 2f(x)-f(1/x)=2x^2-1. Tính f(7)
Cho x=7 ta có:\(y=f\left(7\right)=2f\left(7\right)-f\left(\frac{1}{7}\right)=2.7^2-1=97\)
Vậy \(f\left(7\right)=97\)
Hình như đề sai thì phải bạn ak
cho mk hỏi phân thức \(\frac{x^2-2017}{1+x^{2018}}\) được xác định khi
Cho hàm số f(x) với x > 0. Biết rằng với mọi x lớn hơn 0 thì ta luôn có f(x) - 2f(\(\frac{1}{x}\)) = x - 1. Tính f(3)
\(f\left(\frac{1}{3}\right)-2f\left(3\right)=\frac{1}{3}-1=-\frac{2}{3}\Leftrightarrow f\left(\frac{1}{3}\right)=2f\left(3\right)-\frac{2}{3}\)
\(f\left(3\right)-2f\left(\frac{1}{3}\right)=3-1=2\Rightarrow f\left(3\right)-2.\left[2f\left(3\right)-\frac{2}{3}\right]=2\Leftrightarrow-3.f\left(3\right)=2-\frac{4}{3}=\frac{2}{3}\Leftrightarrow f\left(3\right)=-\frac{2}{9}\)
Cho hàm số f(x) với x > 0. Biết rằng với mọi x lớn hơn 0 thì ta luôn có f(x) - 2f(\(\frac{1}{x}\)) = x - 1. Tính f(3)
Cho hàm số f(x) thỏa mãn ∫ 0 1 ( x + 1 ) f ' ( x ) d x = 10 và 2f(1) – f(0) = 2. Tính I = ∫ 0 1 f ( x ) d x
A. I = -12.
B. I = 8.
C. I = 12.
D. I = -8.
Chọn D.
Đặt u = x + 1 d v = f ' ( x ) d x ⇒ d u = d x v = ∫ f ' ( x ) d x
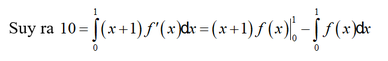
⇔ 10 = 2f(1) – f(0) – I ⇔ 10 = 2 – I ⇔ I = -8.
cho hàm số f(x) xác định với mọi x thỏa mãn f(X) +2f(1/x) = X^2 tính f(1/3)
hàm số f(x) xác định với mọi x thỏa mãn \(f\left(x\right)+2f\left(\frac{1}{x}\right)=x^2\)nên:
+) x = 3 thì \(f\left(3\right)+2f\left(\frac{1}{3}\right)=\frac{1}{9}\Rightarrow2f\left(3\right)+4f\left(\frac{1}{3}\right)=\frac{2}{9}\)(1)
+) x = \(\frac{1}{3}\)thì \(f\left(\frac{1}{3}\right)+2f\left(3\right)=9\)(2)
Lấy (1) - (2) ta được: \(3f\left(\frac{1}{3}\right)=\frac{-79}{9}\)
\(\Rightarrow f\left(\frac{1}{3}\right)=\frac{-79}{27}\)
Làm ngược, sửa:))
+) Nếu x = 3 thì \(f\left(3\right)+2f\left(\frac{1}{3}\right)=9\Rightarrow2f\left(3\right)+4f\left(\frac{1}{3}\right)=18\)(1)
+) Nếu x = \(\frac{1}{3}\) thì \(f\left(\frac{1}{3}\right)+2f\left(3\right)=\frac{1}{9}\)(2)
Lấy (1) - (2) ta được: \(3f\left(\frac{1}{3}\right)=\frac{161}{9}\)
\(\Rightarrow f\left(\frac{1}{3}\right)=\frac{161}{7}\)