Xx6+x:3=1/2
Bạn nào biết làm bài này thì giúp mình nhé
Có bạn nào biết làm câu này không thì giúp mình nha mình đang cần gấp 9 giờ mình phải nộp cho cô rồi nếu được thì mình cảm ơn nhiều chỉ phải làm câu 3 bài 1 thôi nhé
O1=O2( vì 2 góc đối đỉnh)
O3 và O4 thì làm theo cách hai góc kề bù
Vd :O1+O3=180 độ (2 góc kề bù)
Suy ra :120 độ +O3=180 độ
Vậy từ đó tính ra đc O3 ,tương tự O4 cũng vậy
Bạn nào biết làm bài này thì giúp mình nhé
What ????? Đề đâu ?
Chúc bạn : Hok_Ngu
#Thiên_Hy
bài giải;
bài giải đây nè
đáp số:bài giải đây nè.

Các bạn giúp mình làm những bài này gấp nhé ! Các bạn biết làm bài nào thì giúp mình bài nấy nhé . Mình cám ơn rất nhiều ^^
Bài 2:
Đặt \(\frac{a}{b}=\frac{c}{d}=k\Rightarrow\begin{cases}a=kb\\c=kd\end{cases}\)
=> \(\frac{5a+3b}{5a-3b}=\frac{5kb+3b}{5kb-3b}=\frac{b\left(5k+3\right)}{b\left(5k-3\right)}=\frac{5k+3}{5k-3}\left(1\right)\)
\(\frac{5c+3d}{5c-3d}=\frac{5kd+3d}{5kd-3d}=\frac{d\left(5k+3\right)}{d\left(5k-3\right)}=\frac{5k+3}{5k-3}\left(2\right)\)
Từ (1) và (2) => \(\frac{5a+3b}{5a-3b}=\frac{5c+3d}{5c-3d}\)
Bài 3:
Đặt \(\frac{a}{b}=\frac{b}{c}=\frac{c}{d}=k\)
=> \(\frac{a}{b}.\frac{b}{c}.\frac{c}{d}=k^3\)
=> \(\frac{a}{d}=k^3\) (1)
Lại có: \(\frac{a+b+c}{b+c+d}=\frac{a}{b}=\frac{b}{c}=\frac{c}{d}=k\)
=> \(\left(\frac{a+b+c}{b+c+d}\right)^3=k^3\) (2)
Từ (1) và (2) => \(\frac{a}{d}=\left(\frac{a+b+c}{b+c+d}\right)^3\)
Bài 1: Ta có:
\(\frac{a+b-c}{c}=\frac{a-b+c}{b}=\frac{-a+b+c}{a}\)
\(=\frac{a+b}{c}-\frac{c}{c}=\frac{a+c}{b}-\frac{b}{b}=\frac{b+c}{a}-\frac{a}{a}\)
\(=\frac{a+b}{c}-1=\frac{a+c}{b}-1=\frac{b+c}{a}-1\)
\(\Rightarrow\frac{a+b}{c}=\frac{a+c}{b}=\frac{b+c}{a}\) (1)
Xét 2 trường hợp
Nếu a + b + c = 0 \(\Rightarrow\begin{cases}a+b=-c\\a+c=-b\\b+c=-a\end{cases}\)\(\Rightarrow\frac{\left(a+b\right).\left(b+c\right).\left(a+c\right)}{abc}=\frac{-c.\left(-b\right).\left(-a\right)}{abc}=-1\)
Nếu a + b + c \(\ne0\)Áp dụng tính chất của dãy tỉ số = nhau ta có:
\(\frac{a+b}{c}=\frac{a+c}{b}=\frac{b+c}{a}=\frac{\left(a+b\right)+\left(a+c\right)+\left(b+c\right)}{c+b+a}=\frac{2.\left(a+b+c\right)}{a+b+c}=2\)
\(\Rightarrow\frac{\left(a+b\right)\left(b+c\right)\left(a+c\right)}{abc}=2^3=8\)
Mn giải giúp mình đề này với, ai làm được bài nào thì giúp mình luôn nhé. cám ơn mn
Bạn nào biết làm thì giúp mình 3 bài này nha mình đang cần gấp 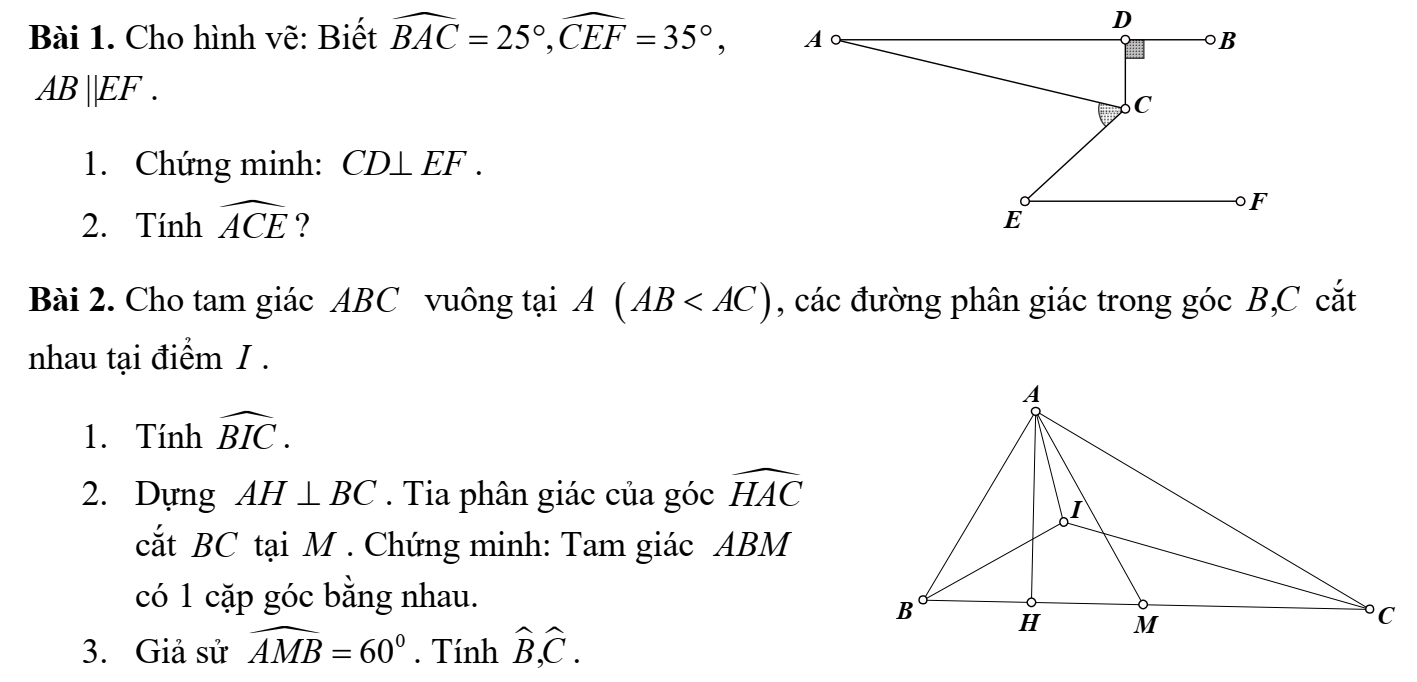
a ...13 chia hết cho 3 là:
b 1...8 chia hết cho 9 là:
c 36... chia hết cho 3và5 là:
d 891... chia hết cho 2,3,5 và 9 là;
[mong các bn giúp mk]
[ bài này ở cùng em học toán lop 5 tập 2bạn nào làm xong tuần 29 làm nốt giúp mk nhé ]
Cảm Ơn
a ...13 chia hết cho 3 là:213,513,723
b 1...8 chia hết cho 9 là:108,198
c 36... chia hết cho 3và5 là:360
d 891... chia hết cho 2,3,5 và 9 là;8910
a. 513 chia hết cho 3
b. 108 chia hết cho 9
c 360 chia hết cho 3 và 5
d 8910 chia hết cho 2 , 3 , 5 và 9
Có bạn nào biết làm câu này không thì giúp mfinh nha mình đang cần gấp 9 giờ mình phải nộp cho cô rồi nếu đươc mình cảm ơn nhiều chỉ phải làm bài 1 thôi nhé!
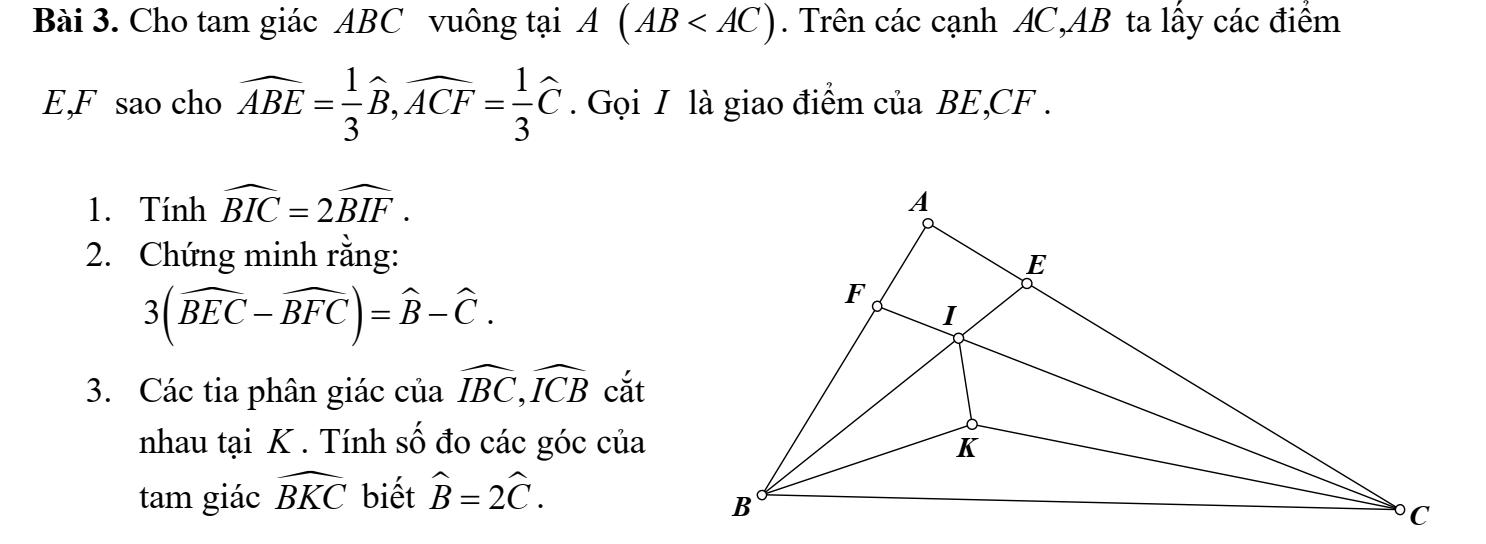
Các bạn làm giúp mình 3 bài này nhé, bài nào cũng dc, chú ý ghi rõ cách làm
CÁC BẠN GIÚP MÌNH BÀI NÀY NHÉ
Tìm x, biết
a) ( x - 1 )3 + 3( x + 1)2 = ( x2 - 2x + 4 )( x + 2)
b) x2 - 4 = 8( x - 2 )
GIÚP MÌNH NHÉ DẠO NÀY CHẲNG BẠN NÀO GIÚP MÌNH BUỒN QUÁ
a) \(\left(x-1\right)^3+3\left(x+1\right)^2=\left(x^2-2x+4\right)\)
\(\Leftrightarrow x^3+9x+2=x^3+8\)
\(\Leftrightarrow x^3+9x=x^3+8-2\)
\(\Leftrightarrow x^3+9x=x^3+6\)
\(\Leftrightarrow x^3+9x=x^3+6x-x^3\)
\(\Leftrightarrow\frac{2}{3}\)
b) \(x^2-4=8\left(x-2\right)\)
\(\Leftrightarrow x^2-4=8x-16\)
\(\Leftrightarrow x^4-4=8x-16+16\)
\(\Leftrightarrow x^2+12=8x\)
\(\Leftrightarrow x^2+12=8x-8x\)
\(\Leftrightarrow x^2-8x+12=0\)
\(\Rightarrow\orbr{\begin{cases}x=2\\x=6\end{cases}}\)