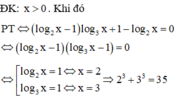Giải phương trình: log2x.log3x + x.log3x + 3 = log2x + 3log3x + x. Tổng tất cả các nghiệm bằng ?

Những câu hỏi liên quan
Giải phương trình log2x.log3x + x.log3x + 3 log2x + 3log3x + x . Ta có tổng các nghiệm là A. 35 B. 9 C. 5 D. 10
Đọc tiếp
Giải phương trình log2x.log3x + x.log3x + 3 = log2x + 3log3x + x . Ta có tổng các nghiệm là
A. 35
B. 9
C. 5
D. 10
Chọn C.
Điều kiện x > 0
Phương trình tương đương:
log2x( log3x - 1) + x( log3x - 1) - 3(log3x - 1) = 0
Hay ( log3x - 1) ( log2 x + x - 3) = 0
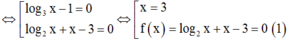
Ta có ![]() đồng biến với x > 0
đồng biến với x > 0
Suy ra (1) có nghiệm thì là nghiệm duy nhất, dễ thấy (1) có nghiệm x = 2
Suy ra 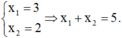
Đúng 0
Bình luận (0)
Giải phương trình
log
2
x
.
log
3
x
+
x
.
log
3
x
+
3
log
2
x
+
3
log
3
x
+
x
.
Ta có tổng các nghiệm là A. 35 B. 9 C. 5 D. 10
Đọc tiếp
Giải phương trình log 2 x . log 3 x + x . log 3 x + 3 = log 2 x + 3 log 3 x + x . Ta có tổng các nghiệm là
A. 35
B. 9
C. 5
D. 10
Tính tổng lập phương các nghiệm của phương trình: log 2 x . log 3 x + 1 = log 2 x + log 3 x
A. 125
B. 35
C. 13
D. 5
Tính tổng lập phương các nghiệm của phương trình: log 2 x . log 3 x + 1 = log 2 x + log 3 x
A. 125
B. 35
C. 13
D. 5
Đáp án B
Phương pháp:
Đưa phương trình về dạng tích sau đó giải phương trình logarit cơ bản.
Cách giải:
ĐKXĐ: x > 0
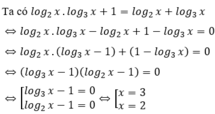
Tổng lập phương các nghiệm của phương trình là: 33 + 23 = 35
Đúng 0
Bình luận (0)
Đặt T là tổng bình phương tất cả các nghiệm của phương trình
1
6
−
log
2
4
x
+
2
2
+
log
2
x
1.
Vậy T bằng A. 6 B. 20 C. 36 D. 2
Đọc tiếp
Đặt T là tổng bình phương tất cả các nghiệm của phương trình
1
6
−
log
2
4
x
+
2
2
+
log
2
x
=
1.
Vậy T bằng
A. 6
B. 20
C. 36
D. 2
Đáp án B
Điều kiện:
x > 0 log 2 4 x ≠ 6 log 2 x ≠ − 2 ⇔ x > 0 x ≠ 16 x ≠ 1 4 .
1 6 − log 2 4 x + 2 2 + log 2 x = 1 ⇔ 1 4 − log 2 x + 2 2 + log 2 x = 1 ⇔ 2 + log 2 x + 8 − 2 log 2 x 4 − log 2 x 2 + log 2 x = 1 ⇔ 10 − log 2 x = − log 2 2 x + 2 log 2 x + 8 ⇔ − log 2 2 x + 3 log 2 x − 2 = 0 ⇔ log 2 x = 1 log 2 x = 2 ⇔ x = 2 x = 4 .
Vậy tổng bình phương tất cả các nghiệm của phương trình bằng 20
Đúng 0
Bình luận (0)
Số nghiệm nguyên của bất phương trình
log
2
x
+
log
3
x
⩾
1
+
log
2
x
.
log
3
x
là A. 1 B. 2 C. 3 D. 4
Đọc tiếp
Số nghiệm nguyên của bất phương trình log 2 x + log 3 x ⩾ 1 + log 2 x . log 3 x là
A. 1
B. 2
C. 3
D. 4
Số nghiệm nguyên của bất phương trình log2x + log3x ≥ 1 + log2x.log3x là
A. 1
B. 2
C. 3
D. vô số
Đáp án B
ĐK: ![]()
![]()
Phương trình có 2 nghiệm nguyên là x = 2; x = 3
Đúng 0
Bình luận (0)
Tích tất cả các nghiệm của phương trình
l
o
g
2
2
x
+
(
x
-
1
)
l
o
g
2
x
6
-
2
x
bằng: A.
2
-
1
. B. 2. C. -1 D. 1.
Đọc tiếp
Tích tất cả các nghiệm của phương trình l o g 2 2 x + ( x - 1 ) l o g 2 x = 6 - 2 x bằng:
A. 2 - 1 .
B. 2.
C. -1
D. 1.
Tích tất cả các nghiệm của phương trình
log
2
2
x
+
log
2
x
+
1
1
bằng A.
2
-
1
-
5
2
B. 1 C.
2...
Đọc tiếp
Tích tất cả các nghiệm của phương trình log 2 2 x + log 2 x + 1 = 1 bằng
A. 2 - 1 - 5 2
B. 1
C. 2 1 - 5 2
D. 1 5