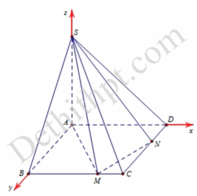
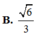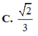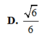cho hình chóp S.ABCD có đáy là hình vuông canh a, SA vuông (ABCD). gọi M,N là 2 điểm lần lượt nằm trên cạnh BC và DC sao cho BM=a/3a/4. CMR: (SMN) vuông (SAM)

Những câu hỏi liên quan
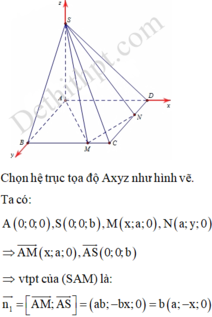
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD); M, N là hai điểm nằm trên hai cạnh BC, CD. Đặt
B
M
x
,
D
N
y
0
x
,
y
a
.
Hệ thức liên hệ giữa x và y để hai mặt phẳng (SAM) và (SMN) vuông góc với nhau là: A. ...
Đọc tiếp
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD); M, N là hai điểm nằm trên hai cạnh BC, CD. Đặt B M = x , D N = y 0 < x , y < a . Hệ thức liên hệ giữa x và y để hai mặt phẳng (SAM) và (SMN) vuông góc với nhau là:
A. x 2 + a 2 = a x + 2 y .
B. x 2 + a 2 = a x + y .
C. x 2 + 2 a 2 = a x + y .
D. 2 x 2 + a 2 = a x + y .
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD); M, N là hai điểm nằm trên hai cạnh BC, CD. Đặt BMx, DNy (0x,ya). Hệ thức liên hệ giữa x và y để hai mặt phẳng (SAM) và (SMN) vuông góc với nhau là:
Đọc tiếp
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD); M, N là hai điểm nằm trên hai cạnh BC, CD. Đặt BM=x, DN=y (0<x,y<a). Hệ thức liên hệ giữa x và y để hai mặt phẳng (SAM) và (SMN) vuông góc với nhau là:
![]()
![]()
![]()
![]()
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, SA ⊥ (ABCD) và S A = a 15 Gọi M, N lần lượt là trung điểm của BC và CD: Tính khoảng cách từ điểm C đến mặt phẳng (SMN)?
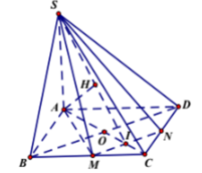
Gọi I = AC ∩ MN ⇒ I là trung điểm của OC, ta có:
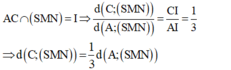
- Ta có: MN// BD mà BD ⊥ (SAC)(cmt) ⇒ MN ⊥ (SAC).
- Trong (SAC) kẻ AH ⊥ SI (H ∈ SI) ⇒ MN ⊥ AH.
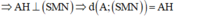
- Ta có:
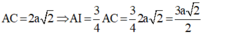
- Xét tam giác vuông SAI ta có:
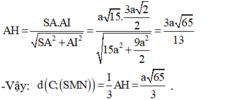
Đúng 0
Bình luận (0)
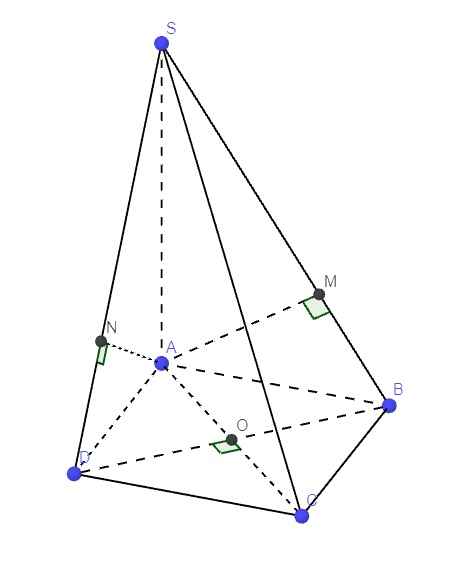
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, cạnh bên SA vuông góc với đáy và SA=3a. Gọi M,N lần lượt là hình chiếu của A trên SB,SD.
a, Cmr: SC vuông góc với mpAMN
b, Tính chu vi tam giác AMN
Mn giải giúp em với ạ
a.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp AM\)
Mà \(AM\perp SB\)
\(\Rightarrow AM\perp\left(SBC\right)\Rightarrow AM\perp SC\) (1)
Hoàn toàn tương tự, ta có \(AN\perp\left(SCD\right)\Rightarrow AN\perp SC\) (2)
(1);(2) \(\Rightarrow SC\perp\left(AMN\right)\)
b.
\(SB=SD=\sqrt{SA^2+AB^2}=a\sqrt{13}\)
Áp dụng hệ thức lượng trong tam giác vuông SAB:
\(AM=\dfrac{SA.AB}{SB}=\dfrac{6a\sqrt{13}}{13}\)
Hệ thức lượng tam giác vuông SAD:
\(AN=\dfrac{SA.AD}{SD}=\dfrac{6a\sqrt{13}}{13}\)
\(\Rightarrow AM=AN\Rightarrow SM=SN=\sqrt{SA^2-AM^2}=\dfrac{9a\sqrt{13}}{13}\)
\(\Rightarrow\dfrac{SM}{SB}=\dfrac{SN}{SD}\Rightarrow MN||BD\Rightarrow\dfrac{MN}{BD}=\dfrac{SM}{SB}\)
\(\Rightarrow MN=\dfrac{SM.BD}{SB}=\dfrac{18a\sqrt{2}}{13}\)
\(\Rightarrow AM+AN+MN=...\)
Đúng 0
Bình luận (0)
Cho hình chóp tứ giác $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$ và $SA$ vuông góc với mặt phẳng $(ABCD)$. Gọi $O$ là trung điểm của cạnh $SC$, $M$, $N$ lần lượt là trung điểm của các cạnh $SB$, $SD$. Gọi $P$ là điểm nằm trên đường thẳng $AN$ sao cho $OP perp AM$. Chứng minh rằng: $$frac{PM}{PN} frac{1}{3}.$$ **Lời giải:** Áp dụng định lí Menelaus lần lượt trên tam giác $ABC$ và $ACD$, ta có: $$frac{SM}{SB}cdot frac{BO}{OC}cdot frac{CQ}{QA} 1,$$ $$frac{SD}{SC}cdot frac{CO}{OB}cdot frac{BP}{...
Đọc tiếp
Cho hình chóp tứ giác $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$ và $SA$ vuông góc với mặt phẳng $(ABCD)$. Gọi $O$ là trung điểm của cạnh $SC$, $M$, $N$ lần lượt là trung điểm của các cạnh $SB$, $SD$. Gọi $P$ là điểm nằm trên đường thẳng $AN$ sao cho $OP \perp AM$. Chứng minh rằng: $$\frac{PM}{PN} = \frac{1}{3}.$$ **Lời giải:** Áp dụng định lí Menelaus lần lượt trên tam giác $ABC$ và $ACD$, ta có: $$\frac{SM}{SB}\cdot \frac{BO}{OC}\cdot \frac{CQ}{QA} = 1,$$ $$\frac{SD}{SC}\cdot \frac{CO}{OB}\cdot \frac{BP}{PA} = 1,$$ trong đó $Q$ là giao điểm của $SN$ và $OM$. Do đó, ta có: $$\frac{SM}{SB} = \frac{SC}{SO},$$ $$\frac{SD}{SC} = \frac{SB}{SO}.$$ Tiếp theo, ta chứng minh $AP \parallel DC$. Ta có $\angle BSA = 90^{\circ}$ và $\angle BSC = \angle DSC$ nên tam giác $BSD$ vuông cân tại $S$. Do đó $SM = NS$. Khi đó, ta có: $$\frac{SM}{SB} = \frac{NS}{NB} = \frac{1}{2}.$$ Từ đó ta suy ra $\frac{SC}{SO} = \frac{1}{2}$, hay $SO = 2SC$. Áp dụng định lí Pythagore trong tam giác $SBO$ ta có: $SB = \sqrt{2}a$. Mặt khác, ta có $OM = \frac{1}{2}a$ và $OS = \frac{2}{3}SC = \frac{1}{3}a$, suy ra $BM = \frac{\sqrt{2}}{2}a$ và $BO = \frac{\sqrt{6}}{2}a$. Áp dụng định lí Pythagore trong tam giác $SDO$ ta có: $SD = \sqrt{6}a$. Mặt khác, ta có $ON = \frac{1}{2}a$ và $OS = \frac{2}{3}SC = \frac{1}{3}a$, suy ra $DN = \frac{\sqrt{2}}{2}a$ và $DO = \frac{\sqrt{6}}{2}a$. Ta có $AP \parallel DC$ khi và chỉ khi: $$\frac{BP}{PA} = \frac{AD}{DC} = \sqrt{2} - 1,$$ trong đó ta đã sử dụng tính chất hình học của hình vuông. Từ định lí Menelaus cho tam giác $ACD$, ta có: $$\frac{AD}{CD}\cdot \frac{CP}{PA}\cdot \frac{NB}{ND} = 1.$$ Do đó, ta có: $$\frac{BP}{PA} = \frac{AD}{CD}\cdot \frac{ND}{NB} = (\sqrt{2} - 1)\cdot \frac{\frac{1}{2}a}{\frac{\sqrt{2}}{2}a} = \frac{2 - \sqrt{2}}{2}.$$ Ta cũng có thể tính được $\frac{PM}{PN}$ bằng cách sử dụng định lí Menelaus cho tam giác $ANB$: $$\frac{AP}{PB}\cdot \frac{MB}{MN}\cdot \frac{SN}{SA} = 1,$$ từ đó ta có: $$\frac{PM}{PN} = \frac{SN}{SM}\cdot \frac{PB}{PA}\cdot \frac{MB}{NB} = \frac{2}{1}\cdot \frac{2 - \sqrt{2}}{2}\cdot \frac{\frac{\sqrt{2}}{2}a}{\frac{\sqrt{2}}{2}a} = \frac{1}{3}.$$ Vậy $\frac{PM}{PN} = \frac{1}{3}$, ta đã chứng minh được bài toán.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tâm 0; cạnh bên SA vuông góc với mặt phẳng (ABCD) và SA=a. Gọi M,N lần lượt là trung điểm của SD và BC. Tính khoảng cách từ điểm M đến mặt phẳng (SBC)
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B,ABBCa,AD2a, cạnh bên SA vuông góc với mặt phẳng đáy,SA3a. Gọi M,N lần lượt là trung điểm của SA, SD. Thể tích của khối đa diện ABCDNMlà
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B,AB=BC=a,AD=2a, cạnh bên SA vuông góc với mặt phẳng đáy,SA=3a. Gọi M,N lần lượt là trung điểm của SA, SD. Thể tích của khối đa diện ABCDNMlà
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a. Góc (BAD)= 60. Tam giác SAD là tam giác cân đỉnh S và nằm trong mặt phẳng vuông góc với đáy, SA= \(\dfrac{a\sqrt{5}}{4}\) Gọi M, N, P lần lượt là trung điểm AD, DC và SB
a, Chứng minh SM ⊥ (ABCD), (SBD) ⊥ (SMN)
b, Tính góc giữa M và (SAC)
Cho hình chóp S.ABCD có đáy là hình thang vuông tại C và D, AD 3a, BC CD 4a; cạnh bên SA vuông góc với đáy và
S
A
a
3
. Gọi M là điểm nằm trên cạnh AD sao cho AM a và N là trung điểm của CD. Gọi α là số đo của góc giữa hai đường thẳng SM và BN. Khi đó cosα bằng A.
5
5
B.
6
3
C.
2...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thang vuông tại C và D, AD = 3a, BC = CD = 4a; cạnh bên SA vuông góc với đáy và S A = a 3 . Gọi M là điểm nằm trên cạnh AD sao cho AM = a và N là trung điểm của CD. Gọi α là số đo của góc giữa hai đường thẳng SM và BN. Khi đó cosα bằng
A. 5 5
B. 6 3
C. 2 3
D. 6 6
Cho hình chóp S.ABCD có đáy là hình thang vuông tại C và D,
A
D
3
a
,
B
C
C
D
4
a
; cạnh bên SA vuông góc với đáy và
S
A
a
3
. Gọi M là điểm nằm trên cạnh AD sao cho
A
M
a
và N là trung điểm của CD. Gọi
α
là số đo của góc giữa hai đường thẳng SM và...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thang vuông tại C và D, A D = 3 a , B C = C D = 4 a ; cạnh bên SA vuông góc với đáy và S A = a 3 . Gọi M là điểm nằm trên cạnh AD sao cho A M = a và N là trung điểm của CD. Gọi α là số đo của góc giữa hai đường thẳng SM và BN. Khi đó cos α bằng