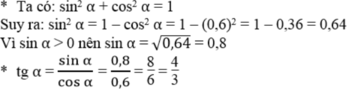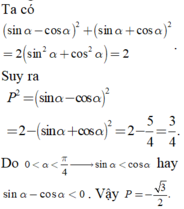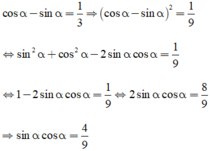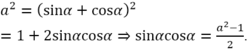cho sin α = 0,6 ; π < α < \(\frac{3\pi}{2}\). tìm cosα , tanα , cotα

Những câu hỏi liên quan
cho góc nhọn α, biết sin α = 0,6 .Không tính số đo góc α, hãy tính cos α, tan α, cot α
\(\sin^2\alpha+\cos^2\alpha=1\\ \Rightarrow\cos^2\alpha=1-0,6^2=0,64\\ \Rightarrow\cos\alpha=0,8=\dfrac{4}{5}\\ \tan\alpha=\dfrac{\sin\alpha}{\cos\alpha}=\dfrac{0,6}{0,8}=\dfrac{3}{4}\\ \cot\alpha=\dfrac{1}{\tan\alpha}=\dfrac{1}{0,75}=\dfrac{4}{3}\)
Đúng 1
Bình luận (0)
Hãy tính sin α và tg α nếu: cos α = 0,6
Các bạn trả lời nhanh giúp mình nhé. Mk đang cần gấp lắm.---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- 1. Tính tỉ số lượng giác của góc nhọn α ( alpha nha )biết:a) sin α 0,8b) tan α 0,6c) Câu này hơi khó hơn (sin α + cos α)/ (sin α - cos) α. Nếu các bạn k hiểu thì trả lời cho mình biết nhé
Đọc tiếp
Các bạn trả lời nhanh giúp mình nhé. Mk đang cần gấp lắm.
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
1. Tính tỉ số lượng giác của góc nhọn α ( alpha nha )biết:
a) sin α = 0,8
b) tan α = 0,6
c) Câu này hơi khó hơn (sin α + cos α)/ (sin α - cos) α. Nếu các bạn k hiểu thì trả lời cho mình biết nhé
ta co \(sin^2a+cos^2a=1\Rightarrow cosa=0.36\)
\(\frac{sina}{cosa}=tana\Rightarrow tana=\frac{20}{9}\)
\(tana\cdot cotga=1\Rightarrow cotga=\frac{9}{20}\)
câu b tương tự nha cau c \(\frac{sina+cosa}{sina-cosa}=\) bn
Đúng 0
Bình luận (0)
bài 1: a)biết sin α=√3/2.tính cos α,tan α,cot α
b)cho tan α=2.tính sin α,cos α,cot α
c)biết sin α=5/13.tính cos,tan,cot α
bài 2
biết sin α x cos α=12/25.tính sin,cos α
1:
a: sin a=căn 3/2
\(cosa=\sqrt{1-sin^2a}=\sqrt{1-\dfrac{3}{4}}=\sqrt{\dfrac{1}{4}}=\dfrac{1}{2}\)
\(tana=\dfrac{\sqrt{3}}{2}:\dfrac{1}{2}=\sqrt{3}\)
cot a=1/tan a=1/căn 3
b: \(tana=2\)
=>cot a=1/tan a=1/2
\(1+tan^2a=\dfrac{1}{cos^2a}\)
=>\(\dfrac{1}{cos^2a}=5\)
=>cos^2a=1/5
=>cosa=1/căn 5
\(sina=\sqrt{1-cos^2a}=\sqrt{\dfrac{4}{5}}=\dfrac{2}{\sqrt{5}}\)
c: \(cosa=\sqrt{1-\left(\dfrac{5}{13}\right)^2}=\dfrac{12}{13}\)
tan a=5/13:12/13=5/12
cot a=1:5/12=12/5
Đúng 0
Bình luận (0)
Cho góc
α
cho thỏa 0
α
π
4
và sin
α
+ cos
α
5
2
Tính P sin
α
-cos
α
.
Đọc tiếp
Cho góc α cho thỏa 0 < α < π 4 và sin α + cos α = 5 2 Tính P = sin α -cos α .
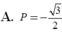
![]()
![]()
![]()
Cho sin α + cos α=√2
a, Tính cos α, sin α, tan α, cot α
b, Tính F = \(sin^5\alpha+cos^5\alpha\)
Cho góc nhọn α. Biết sin α · cos α = 12 / 25 , tính sin α, cos α, tan α.
Ta có : P = sin3 α + cos3 α = ( sinα + cosα) 3 - 3sin α.cosα(sinα + cosα)
Ta có (sin α + cos α) 2 = sin2α + cos2α + 2sinα.cosα = 1 + 24/25 = 49/25.
Vì sin α + cosα > 0 nên ta chọn sinα + cosα = 7/5.
Thay vào P ta được
Cho góc nhọn α biết rằng cos α - sin α = 1/3 . Giá trị của sin α .cos α là
A. 2 3
B. 3 2
C. 4 9
D. 9 4
Cho biết 0≤α≤π20≤α≤π2 sao cho
sin3(α)+cos3(α)=1sin3(α)+cos3(α)=1
Và β=sin(α)+cos(α)β=sin(α)+cos(α)
a) Tính ∑α=07π2(sin−1(β)+α)∑α=07π2(sin−1(β)+α)
b) Chứng minh rằng số ββ thỏa đề bài là nghiệm của phương trình: β3−6β+5=0
Cho biết sin
α
+cos
α
a. Giá trị của sin
α
.cos
α
bằng bao nhiêu? A. sinα.cosα a2. B. sinα.cosα 2a. C.
sin
α
.
cos
α
1
-
a
2
2
D.
sin
α
.
cos
α...
Đọc tiếp
Cho biết sin α +cos α = a. Giá trị của sin α .cos α bằng bao nhiêu?
A. sinα.cosα = a2.
B. sinα.cosα = 2a.
C. sin α . cos α = 1 - a 2 2
D. sin α . cos α = a 2 - 1 2