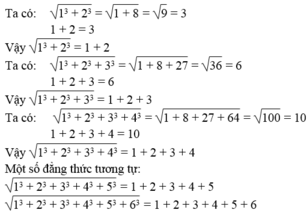Chứng minh bằng qui nạp toán học: 13+23+33+...+n3=(1+2+3+...+n)2 với n\(\ge\)1

Những câu hỏi liên quan
Chứng minh bằng phương pháp quy nạp toán học: \(\forall n\in N\)*, n>1; ta có: \(\dfrac{1}{n+1}+\dfrac{1}{n+2}+...+\dfrac{1}{2n}>\dfrac{13}{24}\)
Chứng minh các đẳng thức sau (
v
ớ
i
n
∈
N
*
)
1
3
+
2
3
+
3
3
+
.
.
.
+
n
3...
Đọc tiếp
Chứng minh các đẳng thức sau ( v ớ i n ∈ N * ) 1 3 + 2 3 + 3 3 + . . . + n 3 = n 2 n + 1 2 4
Đặt vế trái bằng A n
Dễ thấy với n = 1 hệ thức đúng.
Giả sử đã có 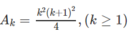
Ta có:
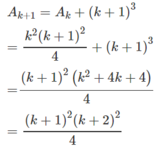
Đúng 0
Bình luận (0)
CHỨNG MINH RẰNG:
Với n thuộc n*:
a, 2\(^n\)> 2n +1 ( n \(\ge\)3 )
b, 3\(^n\)> 3n +1 (n\(\ge\) 2 )
(cm bằng phương pháp qui nạp)
a) GIA SU n=3 (dung) 8>7
gia su dung voi moi k thuocN* (k>=3)
suy ra 2^k>2k+1 (k>=3)
\(2^{k+1}=2^k+2^k\)
<=>\(2^{k+1}>2\left(2k+1\right)\)
<=>\(2^{k+1}>4k+2\)
(2k>1 voi k>=3)=>\(4k+2>2k+3\)
<=>\(2^{k+1}>2k+3\)dung voi moi k thuoc N* (k>=3)
b) tuong tu
Đúng 0
Bình luận (0)
(n+1)(n+2)...(2n) chia hết cho 2^n
(bằng phương pháp qui nạp toán học)
Chứng minh các mệnh đề sau bằng phương pháp qui nạp dãy số:
\(1+\dfrac{1}{2^2}+...+\dfrac{1}{n^2}< 2-\dfrac{1}{n}\forall n\ge2\)
Chứng minh rằng với mọi n thuộc N sao thì
\(n\left(2n^2-3n+1\right)\) chia hết cho 6
( sử dụng phương pháp qui nạp toán học)
\(=n\left(2n^2-2n-n+1\right)\)
\(=n\left(n-1\right)\left(2n-1\right)\)
TH1: n=3k
\(A=3k\left(3k-1\right)\left(6k-1\right)⋮3\)
mà A luôn chia hết cho 2(do n;n-1 là hai số liên tiếp)
nên A chia hết cho 6
TH2: n=3k+1
\(A=\left(3k+1\right)\left(3k+1-1\right)\left(6k+2-1\right)\)
\(=\left(3k+1\right)\left(3k\right)\cdot\left(6k+1\right)⋮3\)
=>A chia hết cho 6
TH3: n=3k+2
\(A=\left(3k+2\right)\left(3k+1\right)\left(6k+4-1\right)\)
\(=\left(3k+2\right)\left(3k+1\right)\left(6k+3\right)⋮6\)
Đúng 0
Bình luận (0)
chứng minh rằng 3^n ≥ 2n+1 với mọi n thuộc N
làm đúng dạng quy nạp toán học mình tích cho
Dễ thấy dấu"=" xảy ra khi x=1
Giả sử bđt đúng với n=k>1 tức là
\(3^k\ge2k+1\) (1)
Nhân cả 2 vế của (1) với 3 ta được
\(3^{k+1}\ge6k+3\Leftrightarrow3^{k+1}\ge3k+4+3k-1\)
Vì 3k-1>0
=>\(3^{k+1}\ge3\left(k+1\right)+1\)
Vậy bđt đúng với n=k+1
=> bđt được chứng minh
Đúng 0
Bình luận (0)
Dễ thấy bất đẳng thức đúng với n = 2
Giả sử bất đẳng thức đúng với n = k ≥ 2, tức là
3k\(\ge\)3k + 1
Nhân hai vế của (1) vơi 3, ta được:
3k + 1 \(\ge\) 9k + 3 <=> 3k + 1 > 3k + 4 + 6k -1.
Vì 6k - 1\(\ge\)0 nên
3k + 1\(\ge\)3k + 4 hay 3k + 1 \(\ge\) 3(k + 1) + 1.
tức là bất đẳng thức đúng với n = k + 1.
Vậy 3n \(\ge\) 3n + 1 với mọi số tự nhiên n
Đúng 0
Bình luận (0)
Chứng minh các mệnh đề sau theo phương pháp qui nạp dãy số:
\(1+\dfrac{1}{2^2}+...+\dfrac{1}{n^2}< 2-\dfrac{1}{n}\forall n\ge2\)
Chứng minh:
1
3
+
2
3
1
+
2
Viết tiếp một số đẳng thức tương tự.
1
3
+
2
3...
Đọc tiếp
Chứng minh: 1 3 + 2 3 = 1 + 2
Viết tiếp một số đẳng thức tương tự.
1 3 + 2 3 + 3 3 = 1 + 2 + 3 1 3 + 2 3 + 3 3 + 4 3 = 1 + 2 + 3 + 4