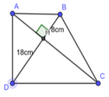
Cho hình thang ABCD vuông tại A và D, hai đường chéo AC và BD vuông góc với nhau. Biết AB = 18cm và CD = 32cm. Khi đó BD = ...

Những câu hỏi liên quan
Cho hình thang ABCD vuông tại A và D, hai đường chéo AC và BD vuông góc nhau.
Biết AB = 18cm và CD = 32cm. Khi đó BD = cm.
Cho hình thang ABCD vuông tại A và D, hai đường chéo AC và BD vuông góc nhau.
Biết AB = 18cm và CD = 32cm. Khi đó AD = cm.
ai cần tham khảo http://olm.vn/hoi-dap/question/355419.html
Đúng 0
Bình luận (0)
bai nay no hoi nhieu rui ma
bik tu hoi nao rui
Đúng 0
Bình luận (0)
TÔI CHƯA HỌC BÀI NÀY
Cho hình thang ABCD vuông tại A và D, hai đường chéo AC và BD vuông góc với nhau. Biết AB= 18cm; CD= 32cm. Khi đó BD=??
Júp mk vs, giải rõ jùm mk vs ạ :)))))))))))))))))DDDDDDDD
Cho hình thang ABCD vuông tại A và D, 2 đường chéo AC và BD vuông góc với nhau. Biết AB = 18cm, CD = 32cm. Tính AC.
Câu 7:
Đường thẳng xy cắt đường tròn (O;7) tại 2 điểm.Khoảng cách d từ O đến xy thuộc khoảng [a;b). Vậy a = ......
Câu 8:
Cho hình thang ABCD vuông tại A và D, hai đường chéo AC và BD vuông góc nhau.
Biết AB = 18cm và CD = 32cm. Khi đó AC = ....... cm.
Dễ thấy :Tam giác OAB ~Tam giác OCD
=> AB/DC = OB/OD = OB.OD/OD^2 = AO^2/OD^2 (Hệ thức lượng trong tam giác)
=> AO/OD = căn(AB/CD)= căn(18/32) = 3/4
Ta có : tanADO = AO/DO = AB/AD
=> AB/AD = 3/4 <=> AD = 4AB/3 = 18.4/3 = 24 (cm)
co AD,DC=>AC
Đúng 0
Bình luận (0)
Trả lời 1 câu được **** 1 phát.
Làm hay 4 phát
Đúng 0
Bình luận (0)
Cho hình thang ABCD vuông tại A và D . Biết AB=18 ; CD=32 , hai đường chéo AC và BD vuông góc với nhau . Tính AC, AD
Dễ thấy :Tam giác OAB ~Tam giác OCD
=> AB/DC = OB/OD = OB.OD/OD^2 = AO^2/OD^2 (Hệ thức lượng trong tam giác)
=> AO/OD = căn(AB/CD)= căn(18/32) = 3/4
Ta có : tanADO = AO/DO = AB/AD
=> AB/AD = 3/4 <=> AD = 4AB/3 = 18.4/3 = 24 (cm)
AC=\(\sqrt{AD^2+DC^2}=40\)
tick nha
Đúng 0
Bình luận (0)
Cho hình thang vuông ABCD (
∠
A
∠
D
90
0
) có hai đường chéo AC và BD vuông góc với nhau tại H. Biết HD 18cm, HB 8cm, tính diện tích hình thang ABCD A. 504
c
m
2
B. 505
c
m
2
C. 506
c
m
2
D. 506
c
m...
Đọc tiếp
Cho hình thang vuông ABCD ( ∠ A = ∠ D = 90 0 ) có hai đường chéo AC và BD vuông góc với nhau tại H. Biết HD = 18cm, HB = 8cm, tính diện tích hình thang ABCD
A. 504 c m 2
B. 505 c m 2
C. 506 c m 2
D. 506 c m 2
Xét ∆ ADB vuông tại A có: AH là đường cao ứng với cạnh huyền BD
⇒ A H 2 = HB. HD = 8.18 HA = 12 (cm) (hệ thức lượng trong tam giác vuông)
Xét ∆ ADC vuông tại D có: DH là đường cao ứng với cạnh huyền AC
⇒ H D 2 = H A . H C ⇒ 18 2 = 12 H C => HC = 27 (cm) (hệ thức lượng trong tam giác vuông)
Ta có: AC = AH + HC = 12 + 27 = 39 cm
BD = BH + HD = 8 + 18 = 26cm
S A B C D = A C . B D 2 = 26.39 2 = 507 c m 2
Đáp án cần chọn là: D
Đúng 0
Bình luận (0)
Cho hình thang ABCD có AB//CD góc A băng 90 độ hai đường chéo AC và BD vuông góc với nhau tại O biết AB=4cm , AD=10cm .Tính AC,BD,BC và diện tích hình thang ABCD .
Xét tam giác \(ABD\)vuông tại \(A\):
\(BD^2=AB^2+AD^2\)(định lí Pythagore)
\(=4^2+10^2=116\)
\(\Rightarrow BD=\sqrt{116}=2\sqrt{29}\left(cm\right)\)
Lấy \(E\)thuộc \(CD\)sao cho \(AE\perp AC\)
Suy ra \(ABDE\)là hình bình hành.
\(AE=BD=2\sqrt{29}\left(cm\right),DE=AB=4\left(cm\right)\).
Xét tam giác \(AEC\)vuông tại \(A\)đường cao \(AD\):
\(\frac{1}{AD^2}=\frac{1}{AE^2}+\frac{1}{AC^2}\Leftrightarrow\frac{1}{AC^2}=\frac{1}{AD^2}-\frac{1}{AE^2}=\frac{1}{100}-\frac{1}{116}=\frac{1}{715}\)
\(\Rightarrow AC=\sqrt{715}\left(cm\right)\)
\(AE^2=ED.EC\Leftrightarrow EC=\frac{AE^2}{ED}=\frac{116}{4}=29\left(cm\right)\)suy ra \(DC=25\left(cm\right)\)
Hạ \(BH\perp CD\).
\(BC^2=HC^2+BH^2=21^2+10^2=541\Rightarrow BC=\sqrt{541}\left(cm\right)\)
\(S_{ABCD}=\left(AB+CD\right)\div2\times AD=\frac{4+25}{2}\times10=145\left(cm^2\right)\)
cho hình thang ABCD vuông tại A và D, hai đường cháo AC và BD vuông góc với nhau. Biết AB=18 và CD=32. khi đó AD=
chỉ cần chứng minh tam giác ABD đồng dạng tam giác DAC
==>\(\frac{AD}{DC}=\frac{AB}{AD}\)
==>\(AD^2=AB\cdot DC\)
LẮP VÀO TÍNH LÀ XONG
Đúng 0
Bình luận (0)
Dân ta phải biết sử ta cái gì không biết thì tra google
Ai đồng ý thì tick mình cái
Đúng 0
Bình luận (0)
AC x BD tại O
COD đồng dạng ABO với k=32/18 =16/9
Gọi OA = x ; OB = y => OC = 16/9 x ; OD = 16/9 y
Pitago OAB => x2 +y2 = 182 (1)
Hệ thức lương ADC vuông tại D ( h2 = b'.c')
\(\left(\frac{16}{9}y\right)^2=x.\frac{16}{9}.x\Leftrightarrow x^2=\frac{16}{9}y^2\)(2)
(1)(2) => \(\frac{25}{9}y^2=18^2\Leftrightarrow y=\frac{18.3}{5}=\frac{54}{5}\)
\(\Leftrightarrow x^2=\frac{16}{9}.\frac{54^2}{25}=\left(\frac{4.54}{3.5}\right)^2\Leftrightarrow x=\frac{72}{5}\)
\(\left(\frac{16}{9}y\right)^2=\frac{16}{9}.x^2\)
Pita go AOD => AD2 = x2 + \(\left(\frac{16}{9}y\right)^2\)= x2 + \(\frac{16}{9}.x^2\)=\(\frac{25}{9}.x^2\)
=>AD = \(\frac{5}{3}x=\frac{5}{3}.\frac{72}{5}=24\)
Đúng 0
Bình luận (0)
Câu 1Cho hình bình hành ABCD có BC 3cm, góc D bằng 65 độ. Kẻ AH vuông góc với CD tại H. Khi đó AH .... cm. (Nhập kết quả đã làm tròn đến chữ số thập phân thứ nhất) Câu 2:Tam giác ABC vuông tại A, biết AB3cm,BC5cm.Đường phân giác ngoài của góc B cắt AC tại N.Khi đó AN..... cm.Câu 3:Cho tam giác đều MNP ngoại tiếp đường tròn bán kính 2cm.Khi đó diện tích tam giác MNP bằngsqrt{a} cm2. Vậy a ....Câu 4:Cho hình thang ABCD vuông tại A và D, hai đường chéo AC và BD vuông góc nhau.Biết AB 18cm và C...
Đọc tiếp
Câu 1
Cho hình bình hành ABCD có BC = 3cm, góc D bằng 65 độ. Kẻ AH vuông góc với CD tại H. Khi đó AH =.... cm. (Nhập kết quả đã làm tròn đến chữ số thập phân thứ nhất)
Câu 2:
Tam giác ABC vuông tại A, biết AB=3cm,BC=5cm.Đường phân giác ngoài của góc B cắt AC tại N.
Khi đó AN=..... cm.
Câu 3:
Cho tam giác đều MNP ngoại tiếp đường tròn bán kính 2cm.
Khi đó diện tích tam giác MNP bằng\(\sqrt{a}\) cm2. Vậy a = ....
Câu 4:
Cho hình thang ABCD vuông tại A và D, hai đường chéo AC và BD vuông góc nhau.
Biết AB = 18cm và CD = 32cm. Khi đó AC =..... cm.
NA/BA = NC/BC
Vì Tam giác ABC vuông tại A, biết AB=3cm,BC=5cm => AC= 4(cm)
=> NC-NA=4 (cm)
=> NC/BC = NA/BA = ( NC-NA)/(BC-AB) = 2
=> NA= BA*2 =6 (cm)
Đúng 0
Bình luận (0)


















