tìm m để biêu thức (m+3)/(m2+m+6) có giá trị nguyên

Những câu hỏi liên quan
tìm giá trị nguyên của m và n để biểu thức :
a) P= 2/6-m có giá trị lớn nhất
b) Q= 8-n/ n-3 có giá trị nhỏ nhất
Tìm các giá trị nguyên của x để phân thức M có giá trị một số nguyên:
M
10
x
2
-
7
x
-
5
2
x
-
...
Đọc tiếp
Tìm các giá trị nguyên của x để phân thức M có giá trị một số nguyên: M = 10 x 2 - 7 x - 5 2 x - 3
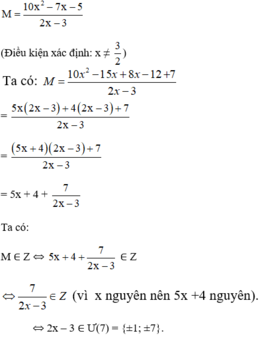
+ 2x – 3 = 1 ⇔ 2x = 4 ⇔ x = 2.
+ 2x – 3 = -1 ⇔ 2x = 2 ⇔ x = 1.
+ 2x – 3 = 7 ⇔ 2x = 10 ⇔ x = 5
+ 2x – 3 = -7 ⇔ 2x = -4 ⇔ x = -2.
Vậy với x ∈ {-2; 1; 2; 5} thì giá trị biểu thức M là một số nguyên.
Đúng 0
Bình luận (0)
Cho phương trình
x
2
– (2m + 1)x +
m
2
+ 1 0, với m là tham số. Tìm tất cả các giá trị của m
∈
ℤ
để phương trình có hai nghiệm phân biệt
x
1
;
x
2
sao cho biểu thức
P
x
1
x...
Đọc tiếp
Cho phương trình x 2 – (2m + 1)x + m 2 + 1 = 0, với m là tham số. Tìm tất cả các giá trị của m ∈ ℤ để phương trình có hai nghiệm phân biệt x 1 ; x 2 sao cho biểu thức P = x 1 x 2 x 1 + x 2 có giá trị là số nguyên
A. m = 1
B. m = 2
C. m = −2
D. m = 0
Cho phương trình x2 - (2m+1)x + m2 +1 = 0 , với m là tham số . Tìm tất cả các giá trị m ∈ Z để phương trình có hai nghiệm phân biệt x1 , x2 sao cho biểu thức \(P=\dfrac{x_1x_2}{x_1+x_2}\)
có giá trị là số nguyên
Đk để pt trên có 2 nghiệm phân biệt x1,x2 : a>0 và denta>0
suy ra denta= (2m+1)^2-4.(m^2+1)>0
suy ra : m>3/4
Ta có P=x1x2/x1+x2=(m^2+1)/(2m+1)
Ta có: P∈Z
⇒4P∈Z
⇒(4m^2+4)/2m+1=(2m-1)+5/2m+1∈Z
⇒2m+1=Ư(5)={−5;−1;1;5}
⇒m={−3;−1;0;2}
Kết hợp đk m>3/4 ta được m=2
Đúng 1
Bình luận (0)
1.Tìm a để đa thức x^3- 7x^2 + a chia hết cho đa thức x -2
2.Cho biểu thức M=x+2/x+3-5/x^2+x-6+1/2-x
a) Tìm ĐKXĐ và rút gọn biểu thức M.
b) Tìm x nguyên để M có giá trị nguyên
\(1.Tìm a để đa thức x^3- 7x^2 + a chia hết cho đa thức x -2 2.Cho biểu thức M=x+2/x+3-5/x^2+x-6+1/2-x a) Tìm ĐKXĐ và rút gọn biểu thức M. b) Tìm x nguyên để M có giá trị nguyên\)
Cho biểu thức M = (\(\frac{4}{x^2-4}-\frac{4}{x+4}\)) . \(\frac{x^2+8x+16}{32}\)
a. Tìm điều kiện x để giá trị M có nghĩa
b. tìm giá trị x để giá trị M= \(\frac{1}{3}\)
c. Tìm giá trị x để M =1
d. Tìm giá trị nguyên x để giá biểu thức M nhận giá trị nguyên
a) \(x\ne2;-2;-4\)
b) và c) thì bạn rút gọn M rồi tính
Đúng 0
Bình luận (0)
Cho biểu thức M=(x/x-3 + 3x2+3/9-x2 + 2x/x+3 ) : x+1/3-x
a, với giá trị nào của x thì M có nghĩa ? Rút gọn M
tính giá trị biểu thức M biết x2+x-6=0
tìm x nguyên để M nguyên
Answer:
\(M=\left(\frac{x}{x-3}+\frac{3x^2+3}{9-x^2}+\frac{2x}{x+3}\right):\frac{x+1}{3-x}\)
ĐKXĐ:
\(x-3\ne0\)
\(9-x^2\ne0\)
\(x+3\ne0\)
\(x+1\ne0\)
(Ý này trình bày trong vở bạn xếp vào vào cái ngoặc "và" nhé!)
\(\Leftrightarrow\hept{\begin{cases}x\ne\pm3\\x\ne-1\end{cases}}\)
\(=\frac{-x\left(3+x\right)+3x^2+3+2x\left(3-x\right)}{\left(3-x\right)\left(3+x\right)}.\frac{\left(3-x\right)}{x+1}\)
\(=\frac{9x+3}{\left(3+x\right)\left(x+1\right)}\)
\(=\frac{3}{x+1}\)
Có: \(x^2+x-6=0\)
\(\Leftrightarrow x^2+6x-x-6=0\)
\(\Leftrightarrow x\left(x+6\right)-\left(x+6\right)=0\)
\(\Leftrightarrow\left(x+6\right)\left(x-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+6=0\\x-1=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-6\\x=1\end{cases}}\) (Thoả mãn)
Trường hợp 1: \(x=1\Leftrightarrow M=\frac{3}{1+1}=\frac{3}{2}\)
Trường hợp 2: \(x=-6\Leftrightarrow M=\frac{3}{-6+1}=\frac{-3}{5}\)
Để cho biểu thức M nguyên thì \(\frac{3}{x+1}\inℤ\)
\(\Rightarrow x+1\inƯ\left(3\right)\)
\(\Rightarrow\orbr{\begin{cases}x+1=1\\x+1=3\end{cases}\Rightarrow\orbr{\begin{cases}x=0\\x=2\end{cases}}}\) (Thoả mãn)
Cho biểu thức
M=căn x +1/2
A)Tìm các giá trị nguyên của x để M nhận giá trị nguyên
B)Tìm giá trị lớn nhất của biểu thức M
c)Tìm các giá trị nguyên của x để A nhận giá trị nguyên
Tìm giá trị nguyên của m và n để biểu thức:
1) P = \(\dfrac{2}{6-m}\)có giá trị lớn nhất.
2) Q = \(\dfrac{8-n}{n-3}\)có giá trị nguyên nhỏ nhất.
1/ Ta có: \(P=\frac{2}{6-m}\)\(\le2\left(\forall m\in Z\right)\)
Dấu "=" xảy ra \(\Leftrightarrow6-m=1\Rightarrow m=5\).
Vậy Max P =2 khi m = 5.
2/ Ta có: \(Q=\frac{8-n}{n-3}\ge0\left(\forall n\in Z\right)\)
Dấu "=" xảy ra \(\Leftrightarrow8-n=0\Rightarrow n=8.\)
Vậy Min Q = 0 khi n = 8.
Chúc bn hc tốt!^_^.
Nhớ kb và cho tớ nhé mọi người!
Đúng 0
Bình luận (1)
1/ta có :2/6-m max
suy ra:6-m>0,6-m min
suy ra:6-m=1
suy ra: m=5
Vậy ...
Đúng 0
Bình luận (0)




















