Thứ 2:CC;Văn;Nhạc;Sử ;CN
Thứ 3:Hóa;Anh;TD;Văn;Sinh
Thứ 4:Sử;Toán;Lí;TCToán;Hóa
Thứ 5:TCHóa;Văn;Toán;Toán
Thứ 6:Anh;TD;Địa;Toán;SH
Thứ 7:Văn;Văn;CD;Sinh;Lí

Những câu hỏi liên quan
Giúp mik với AE ơi , AE vào link này giúp mik bài 5, 5ư6 trang THỨ 2 nhé !! Mik sẽ TIK
file:///C:/Users/DELL/Downloads/KTB%20cu%CC%83%20sau%20ba%CC%80i%20tie%CC%82n%20%C4%91e%CC%82%CC%80%20oclit%20va%CC%80%20tc%20hai%20%C4%91t%20song%20song.pdf
Không thể truy cập vào tệp của bạn
Tệp này có thể đã bị di chuyển, chỉnh sửa hoặc xóa.
ERR_FILE_NOT_FOUND
@Cỏ
#Forever
Trả lời :
Ko mở đc link nha bạn, bạn hãy tải ảnh lên nhé
# Hok tốt !
Ok mik cảm ơn các bn nhiều !!
Xem thêm câu trả lời
1, Tìm 3 số biết tổng của chúng bằng 74. Số thứ 2= 4/3 số thứ 1 và số thứ 2= 3/4 số thứ 3
2, Cho tam giác ABC, trung tuyến AM; O là trung điểm của AM. Đường thẳng d đi qua O vẽ AA' ; BB'; CC' lần lượt vuông góc với d tại A'; B'; C'; Kẻ MM' vuông tại M
a, CM: AA'= (BB'+CC')/2
b, Biết MM'= 2.75 cm, diện tích tứ giác BB'C'C là 24.75 cm vuông. Tính B'; C'
Cho tam giác ABC nhọn, các đường cao AA', BB', CC'', H là trực tâm.
a) Tính tổng \(\frac{HA'}{AA'}+\frac{Hb'}{BB'}+\frac{HC'}{CC'}\)
b) gọi AI là phân giác của tam giác ABC, IM, IN thứ tự là phân giác của góc AIC và ATB. Cmr: AN.BI.CM=BN.IC.AM
c) cmr: \(\frac{\left(AB+BC+CA\right)^2}{AA'^2=BB'^2+CC'^2}\ge4\)
a) Ta có : \(\frac{HA'}{AA'}=\frac{S_{HA'C}}{S_{AA'C}}=\frac{S_{BHA'}}{S_{AA'B}}=\frac{S_{HA'C}+S_{BHA'}}{S_{AA'B}+S_{AA'C}}=\frac{S_{BHC}}{S_{ABC}}\)
Tương tự : \(\frac{HB'}{BB'}=\frac{S_{AHC}}{S_{ABC}};\frac{HC'}{CC'}=\frac{S_{AHB}}{S_{ABC}}\)
\(\Rightarrow\frac{HA'}{AA'}+\frac{HB'}{BB'}+\frac{HC'}{CC'}=1\)
b) Ta có : \(\frac{AN}{BN}=\frac{AI}{BI}\)
mà \(\frac{AI}{CI}=\frac{AM}{BM}\Rightarrow AI=\frac{AM}{CM}.CI\)
\(\Rightarrow\frac{AN}{BN}=\frac{AM}{CM}.\frac{CI}{BI}\Rightarrow AN.CM.BI=BN.AM.CI\)
Đúng 0
Bình luận (0)
vẽ Cx \(\perp\)CC' ; vẽ D đối xứng với A qua Cx ; DA giao điểm Cx tại I
\(\Rightarrow\)CD = AC và tam giác C'CIA là hình chữ nhật
\(\Rightarrow\)CC' = AI = ID ; \(\widehat{BAD}=90^o\)
Ta có BD \(\le\)BC + CD . Dấu " = " xảy ra \(\Leftrightarrow\)\(\Delta BAD\)vuông tại A \(\Rightarrow\)AC = BC
\(\Rightarrow\)BD2 \(\le\)( BC + CD )2
\(\Delta BAD\)vuông tại A \(\Rightarrow\)BD2 = AB2 + AD2
\(\Rightarrow\)AB2 + AD2 \(\le\)( BC + AC )2
\(\Rightarrow\)AD2 \(\le\)( BC + AC )2 - AB2
\(\Rightarrow\)4CC'2 \(\le\)( BC + AC )2 - AB2 . Dấu " = " xảy ra \(\Leftrightarrow\)AC = BC
tương tự , 4BB'2 \(\le\) ( AB + BC )2 - AC2 Dấu " = " xảy ra \(\Leftrightarrow\)AB = BC
4AA'2 \(\le\)( AB + AC )2 - BC2 Dấu " = " xảy ra \(\Leftrightarrow\)AB = AC
Suy ra : \(4\left(AA'^2+BB'^2+CC'^2\right)\le\left(AB+BC+AC\right)^2\)
\(\Rightarrow\)\(\frac{\left(AB+BC+AC\right)^2}{AA'^2+BB'^2+CC'^2}\ge4\)
Dấu " = " xảy ra \(\Leftrightarrow\)AB = BC = AC hay tam giác ABC đều
Đúng 1
Bình luận (1)
Cho hình hộp ABCD. A'B'C'D'. Gọi M, I, J, N, E thứ tự là trung điểm AD, BD', DC', BI, DJ. Mặt phẳng (MNE) cắt CC' tại O. Tính tỉ số CO/CC'
Xem chi tiết
Cho tam giác ABC nhọn, các đường cao AA', BB', CC', H là trực tâm.
a) Tính tổng HA'/AA' + HB'/BB' + HC'/CC'
b) Gọi AI là phân giác của tam giác ABC (I nằm trong ABC); IM, IN thứ tự là phân giác của góc AIC và góc AIB. Chứng minh rằng: AN.BI.CM = BN.CI.AM
c) Tam giác ABC như thế nào thì biểu thức \(\frac{\left(AB+BC+CA\right)^2}{AA'^2+BB'^2+CC'^2}\) đạt giá trị nhỏ nhất?
tự kẻ hình nha bạn
a, có \(\hept{\begin{cases}S_{HBC}=\frac{BC\cdot HA'}{2}\\S_{ABC}=\frac{BC\cdot AA'}{2}\end{cases}}\) \(\Rightarrow\frac{S_{HBC}}{S_{ABC}}=\frac{BC\cdot HA'}{2}\div\frac{BC\cdot AA'}{2}=\frac{HA'}{AA'}\)
có tương tự ta có \(\frac{S_{HAC}}{S_{ABC}}=\frac{HB'}{BB'}\) và \(\frac{S_{HAB}}{S_{ABC}}=\frac{HC'}{CC'}\)
\(\Rightarrow\frac{S_{HAC}+S_{HBC}+S_{HAB}}{S_{ABC}}=\frac{HA'}{AA'}+\frac{HB'}{BB'}+\frac{HC'}{CC'}\)
\(\Rightarrow\frac{HA'}{AA'}+\frac{HB'}{BB'}+\frac{HC'}{CC'}=1\)
để mjnh làm tiếp câu b
b, IN là pg của \(\widehat{AIB}\) (gt)
\(\Rightarrow\frac{NB}{IB}=\frac{NA}{AI}\) (tc)
\(\Rightarrow NB\cdot AI=IB\cdot NA\)
\(\Rightarrow NB\cdot AI\cdot CM=IB\cdot AN\cdot CM\left(1\right)\)
IM là pg của \(\widehat{AIC}\) (gt)
\(\Rightarrow\frac{AM}{AI}=\frac{MC}{IC}\)
\(\Rightarrow AM\cdot IC=AI\cdot CM\)
\(\Rightarrow AM\cdot IC\cdot NB=AI\cdot CM\cdot NB\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow AN\cdot BI\cdot CM=BN\cdot CI\cdot AM\)
máy biến áp 1 pha có điện áp sơ cấp là 110V . Số vòng dây cuộn sơ cấp gấp 4 lần cuộn thứ cấp. Tính điện áp 2 đầu của cuộn thứ cấp
giải giúp mk vs ! mơn cc
môn công nghệ ko phải toán đâu nha
Vì số vòng dây tỉ lệ thuận với điện áp nên
Điện áp 2 dầu của cuộn thứ cấp là
\(U_2=4.U_1\)
\(=4.110=440\left(V\right)\)
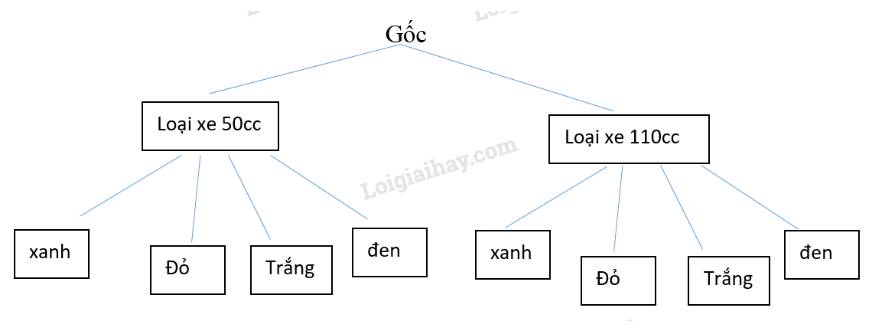
Trong trò chơi Vòng quay may mắn, người chơi sẽ quay hai bánh xe. Mũi tên ở bánh xe thứ nhất có thể dừng ở một trong hai vị trí: Loại xe 50 CC và Loại xe 110 cc. Mũi tên ở bánh xe thứ hai có thể dừng ở một trong bốn vị trí: màu đen, màu trắng, màu đỏ và màu xanh. Vị trí của mũi tên trên hai bánh xe sẽ xác định người chơi nhận được loại xe nào, màu gì. Phép thử T là quay hai bánh xe. Hãy vẽ sơ đồ hình cây mô tả các phần tử của không gian mẫu.
Đọc tiếp
Trong trò chơi "Vòng quay may mắn", người chơi sẽ quay hai bánh xe. Mũi tên ở bánh xe thứ nhất có thể dừng ở một trong hai vị trí: Loại xe 50 CC và Loại xe 110 cc. Mũi tên ở bánh xe thứ hai có thể dừng ở một trong bốn vị trí: màu đen, màu trắng, màu đỏ và màu xanh. Vị trí của mũi tên trên hai bánh xe sẽ xác định người chơi nhận được loại xe nào, màu gì. Phép thử T là quay hai bánh xe. Hãy vẽ sơ đồ hình cây mô tả các phần tử của không gian mẫu.
cho tam giác ABC nhọn, các đường cáo AA', BB', CC', H là trực tâm.
a/ tính tổng \(\frac{HA'}{AA'}+\frac{HB'}{BB'}+\frac{HC'}{CC'}\)
b/ gọi AI là phân giác của tam giác ABC; IM; IN thứ tự là phân giác của góc AIC và góc AIB, chứng minh rằng: AN.BI.CM=BN.IC.AM
c/ tam giác ABC như thế nào thì biểu thức \(\frac{\left(AB+BC+CA\right)^2}{AA'^2+BB'^2+CC'^2}\) đạt giá trị nhỏ nhất?
Cho tam giác ABC, A=120 độ.AA',BB',CC' theo thứ tự là tia phân giác của góc A, B,C. Chứng minh rằng: AA' vuong BB' vuong CC'
Ai giải giúp m vs