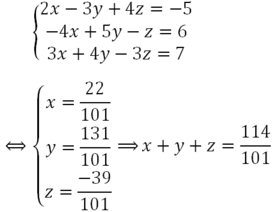cho hệ hương trình kx + y=7
2x - y=-4
gọi (x;y) là nghiệm của hệ hương trình . Xác định giá trị của k để x2 + y2 đạt giá trị nhỏ nhất

Những câu hỏi liên quan
\(\hept{\begin{cases}kx+=7\\2x-y=-4\end{cases}}\)gọi (x;y) là nghiệm của hệ phương trình . xác định giá trị cảu k để P=x2 +y2 đạt giá trị nhỏ nhất ?
cho hệ phương trình: {kx - y + 2 & 3x + ky = 5}
tìm k để hệ phương trình có 1 nghiệm duy nhất (x;y) thỏa mãn x + y < 1
Cho hệ phương trình:
kx+y=7
2x-y=-4
Gọi (x; y) là nghiệm của hệ phương trình . Xác định giá trị của k để P = x 2 + y 2 đạt giá trị nhỏ nhất.
Cho hệ phương trình:
k
x
+
y
7
2
x
-
y
-
4
Gọi (x; y) là nghiệm của hệ phương trình . Xác định giá trị của k để P
x
2
+...
Đọc tiếp
Cho hệ phương trình:
k x + y = 7 2 x - y = - 4
Gọi (x; y) là nghiệm của hệ phương trình . Xác định giá trị của k để P = x 2 + y 2 đạt giá trị nhỏ nhất.
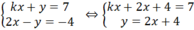
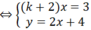
Với k + 2 ≠ 0 ⇔ k ≠ -2 thì hệ phương trình có nghiệm :
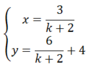
Ta có:
P = x 2 + y 2 = x 2 + 2 x + 4 2
= 5 x 2 + 16 x + 16
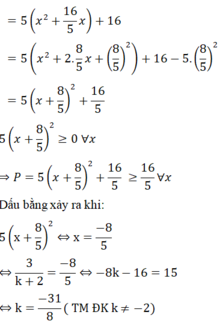
Vậy với k = (-31)/8 thì biểu thức P = x 2 + y 2 đạt giá trị nhỏ nhất
Đúng 0
Bình luận (0)
cho hệ phương trình {a^2x-y=-7 và 2x+y=1
1,giải hệ phương trình khi a=1
2,gọi(x,y)là nghiệm. tìm a để x+y=2
Hai hệ phương trình
k
x
+
3
y
3
-
x
+
y
1
;
x
+
y...
Đọc tiếp
Hai hệ phương trình k x + 3 y = 3 - x + y = 1 ; x + y = 1 - x + y = 1 là tương đương khi k bằng?
A. k = -3
B. k = 1
C. k = 3
D. k = -1
Chọn đáp án C.
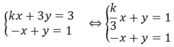
Do đó 2 hệ phương trình 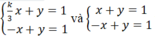 tương đương khi k/3=1 ⇔k=3
tương đương khi k/3=1 ⇔k=3
Đúng 0
Bình luận (0)
Cho hệ phương trình
2
x
-
3
y
+
4
z
-
5
-
4
x
+...
Đọc tiếp
Cho hệ phương trình 2 x - 3 y + 4 z = - 5 - 4 x + 5 y - z = 6 3 x + 4 y - 3 z = 7 . Giả sử (x;y;z) là nghiệm của hệ phương trình, khi đó x+y+z bằng
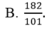
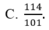
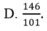
Cho hệ phương trình: \(\hept{\begin{cases}kx-y=5\\x+y=1\end{cases}}\)
a/Với giá trị nào của k thì hệ phương trình có nghiệm là \(\left(x;y\right)=\left(2;-1\right)\)
b/Với giá trị nào của k thì hệ phương trình có nghiệm duy nhất?hệ phương trình vô nghiệm?
a) Ta có hệ phương trình \(\hept{\begin{cases}kx-y=5\\x+y=1\end{cases}}\) Thay nghiệm \(\left(x,y\right)=\left(2,-1\right)\) ta có hệ mới là :
\(\hept{\begin{cases}2k-1=5\\2-1=1\end{cases}\Leftrightarrow k=3}\)
b) Ta có : \(\hept{\begin{cases}kx-y=5\\x+y=1\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=1-x\\kx-1-x=5\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=1-x\\x\left(k-1\right)=6\end{cases}}\)
Để hệ phương trình có nghiệm duy nhất : \(\Leftrightarrow k-1\ne0\) \(\Leftrightarrow k\ne1\)
Để hệ phương trình vô nghiệm \(\Leftrightarrow k-1=0\Leftrightarrow k=1\)
P/s : Em chưa học lớp 9 nên không biết cách trình bày cho lắm :))
cho hệ phương trình mx+2y=1
2x-4y=3
tìm m để hệ phương trình có nghiệm duy nhất (x;y) thỏa mãn x-3y=7/2
Để hệ phương trình có nghiệm duy nhất thì \(\dfrac{m}{2}\ne\dfrac{2}{-4}=-\dfrac{1}{2}\)
=>\(m\ne-1\)
\(\left\{{}\begin{matrix}mx+2y=1\\2x-4y=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2mx+4y=2\\2x-4y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\left(2m+2\right)=5\\2x-4y=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{5}{2m+2}\\4y=2x-3=\dfrac{10}{2m+2}-3=\dfrac{10-6m-6}{2m+2}=\dfrac{-6m+4}{2m+2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{5}{2m+2}\\y=\dfrac{-6m+4}{8m+8}=\dfrac{-3m+2}{4m+4}\end{matrix}\right.\)
x-3y=7/2
=>\(\dfrac{5}{2m+2}-\dfrac{3\cdot\left(-3m+2\right)}{4m+4}=\dfrac{7}{2}\)
=>\(\dfrac{10+3\left(3m-2\right)}{4m+4}=\dfrac{7}{2}\)
=>\(\dfrac{10+9m-6}{4m+4}=\dfrac{7}{2}\)
=>\(\dfrac{9m+4}{4m+4}=\dfrac{7}{2}\)
=>7(4m+4)=2(9m+4)
=>28m+28=18m+8
=>10m=-20
=>m=-2(nhận)
Đúng 1
Bình luận (0)