tam giác ABC nội tiếp đường tròn tâm O .Các điểm M,N,P là điểm chính giữa của các cung AB,BC,CA .Gọi D là giao điểm của MN và AB ,E là giao điểm của PN và AC . Chứng minh DE song song với BC

Những câu hỏi liên quan
Tam giác ABC nội tiếp đường tròn tâm O, các điểm M, N, P là điểm chính giữa của các cung AB, BC, CA. Gọi D là giao điểm của MN và AB, E là giao điểm của PN và AC. Chứng minh rằng DE song song với BC.
Tam giác ABC nội tiếp đường tròn tâm O, các điểm M, N, P là điểm chính giữa của các cung AB, BC, CA. Gọi D là giao điểm của MN và AB, E là giao điểm của PN và AC. Chứng minh rằng DE song song với BC.
Tam giác ABC nội tiếp đường tròn tâm O, các điểm M, N, P là điểm chính giữa của các cung AB, BC, CA. Gọi D là giao điểm của MN và AB, E là giao điểm của PN và AC. Chứng minh rằng DE song song với BC.
Link đây bạn xem thử
http://pitago.vn/question/tam-giac-abc-noi-tiep-duong-tron-tam-o-cac-diem-m-n-p-la-3440.html
Học tốt nhé
Cho tam giác ABC nội tiếp đường tròn ( O ), các điểm M , N , P là các điểm chính giữa của cac cung AB , BC và Ac . Gọi D là giao điểm của MN và Ab , E là giao điểm của PN và AC . Chứng minh : DE song song BC .
cho tam giác ABC ngoại tiếp đường tròn tâm i gọi D ,E ,F lần lượt là các tiếp điểm của các cạnh BC CA AB với đường tròn tâm i .gọi m là giao điểm của AB và BC, AD cắt đường tròn tâm i tại n .gọi k là giao điểm của AC và EF .a)Chứng minh rằng IKND là tứ giác nội tiếp .b) chứng minh rằng MN là tiếp tuyến của đường tròn tâm I.
Cho đường tròn (O) có các dây cung AB, BC, CA. Gọi M là điểm chính giữa của cung nhỏ AB. Vẽ dây MN song song với BC và gọi s là giao điểm của MN và AC. Chứng minh SM = SC và SN = SA
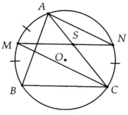
Do sđ M B ⏜ = sđ M A ⏜ = sđ N C ⏜
=> N A S ^ = A N S ^
=> SA = SN => SM = SC
Đúng 0
Bình luận (0)
Cho tam giác ABC nội tiếp (O), I là tâm đường tròn nội tiếp tam giác ABC. AI cắt (O) tại D. Gọi E, F lần lượt là điểm chính giữa các cung AB (không chứa C), AC (không chứa B). M là giao điểm của AB với DE, N là giao điểm của AC với DF. Chứng minh rằng ba điểm M, I, N thẳng hàng.
Cho đường tròn (O;R) đường kính AB. Gọi Ax và By là hai tiếp tuyến của (O); C là một điểm trên đường tròn (O), D là điểm nằm giữa A và O. Đường vuông góc với CD tại C cắt Ax và By lần lượt tại E và F.a. Chứng minh: Tứ giác AECD nội tiếp.b. Gọi M là giao điểm của AC và DE, N là giao điểm của BC và DF. Chứng minh: MN song song với AB.c. Tính tổng diện tích hai hình viên phân giới hạn bởi các cung nhỏ AC và BC với các dây AC và BC của (O) khi ACR?
Đọc tiếp
Cho đường tròn (O;R) đường kính AB. Gọi Ax và By là hai tiếp tuyến của (O); C là một điểm trên đường tròn (O), D là điểm nằm giữa A và O. Đường vuông góc với CD tại C cắt Ax và By lần lượt tại E và F.
a. Chứng minh: Tứ giác AECD nội tiếp.
b. Gọi M là giao điểm của AC và DE, N là giao điểm của BC và DF. Chứng minh: MN song song với AB.
c. Tính tổng diện tích hai hình viên phân giới hạn bởi các cung nhỏ AC và BC với các dây AC và BC của (O) khi AC=R?
Cho tam giác ABC nội tiếp đường tròn (O). E là điểm chính giữa cung BC không chứa
A. Gọi D là giao điểm của AE và BC. Đường thẳng qua D song song với CE cắt BE ở M. Chứng
minh rằng:\(\frac{AB}{AC}=\frac{BM}{EM}\)










