Do sđ M B ⏜ = sđ M A ⏜ = sđ N C ⏜
=> N A S ^ = A N S ^
=> SA = SN => SM = SC
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
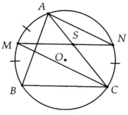
Cho AB, BC, CA là ba dây của đường tròn (O). Từ điểm chính giữa M của cung AB vẽ dây MN song song với dây BC.Gọi giao điểm của MN và AC là S.Chứng minh SM = SC và SN = SA.
Cho AB, BC, CA là ba dây của đường tròn (O). Từ điểm chính giữa M của cung AB vẽ dây MN song song với dây BC.Gọi giao điểm của MN và AC là S.Chứng minh SM = SC và SN = SA.
cho tam giác ABC có ba góc nhọn nôi tiếp trong đường tròn (O).từ điểm M chính giữa cung nhỏ AB kẻ dây MN song song với BC.góc S là giao điểm của MN và AC .chứng minh:SM=SC và SN=SA
Tam giác ABC nội tiếp đường tròn tâm O, các điểm M, N, P là điểm chính giữa của các cung AB, BC, CA. Gọi D là giao điểm của MN và AB, E là giao điểm của PN và AC. Chứng minh rằng DE song song với BC.
Tam giác ABC nội tiếp đường tròn tâm O, các điểm M, N, P là điểm chính giữa của các cung AB, BC, CA. Gọi D là giao điểm của MN và AB, E là giao điểm của PN và AC. Chứng minh rằng DE song song với BC.
Tam giác ABC nội tiếp đường tròn tâm O, các điểm M, N, P là điểm chính giữa của các cung AB, BC, CA. Gọi D là giao điểm của MN và AB, E là giao điểm của PN và AC. Chứng minh rằng DE song song với BC.
Cho tam giác ABC nội tiếp đường tròn ( O ), các điểm M , N , P là các điểm chính giữa của cac cung AB , BC và Ac . Gọi D là giao điểm của MN và Ab , E là giao điểm của PN và AC . Chứng minh : DE song song BC .
Cho đường tròn O và dây cung BC cố định. Trên cung lớn BC lấy điểm A bất kì (A không trùng với B và C), gọi M, N lần lượt là điểm chính giữa cung BC và cung AB. Gọi I là giao điểm của AM và CN, gọi K là giao điểm của MN với AB
a CM:tứ giác ANKI nội tiếp .
b CM:KI song song với BC
Cho đường tròn tâm O bán kính R và hai dây AB, CD bất kì. Gọi M là điểm chính giữa của cung nhỏ AB. Gọi E và F tương ứng là giao điểm của MC, MD với dây AB. Gọi I và J tương ứng là giao điểm của DE, CF với đường tròn (O). Chứng minh IJ song song với AB.