Các câu hỏi tương tự
Cho AB, BC, CA là ba dây của đường tròn (O). Từ điểm chính giữa M của cung AB vẽ dây MN song song với dây BC.Gọi giao điểm của MN và AC là S.Chứng minh SM = SC và SN = SA.
Cho đường tròn (O) có các dây cung AB, BC, CA. Gọi M là điểm chính giữa của cung nhỏ AB. Vẽ dây MN song song với BC và gọi s là giao điểm của MN và AC. Chứng minh SM = SC và SN = SA
cho tam giác ABC có ba góc nhọn nôi tiếp trong đường tròn (O).từ điểm M chính giữa cung nhỏ AB kẻ dây MN song song với BC.góc S là giao điểm của MN và AC .chứng minh:SM=SC và SN=SA
Cho đường tròn tâm O bán kính R và hai dây AB, CD bất kì. Gọi M là điểm chính giữa của cung nhỏ AB. Gọi E và F tương ứng là giao điểm của MC, MD với dây AB. Gọi I và J tương ứng là giao điểm của DE, CF với đường tròn (O). Chứng minh IJ song song với AB.
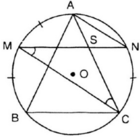
Tam giác ABC nội tiếp đường tròn tâm O, các điểm M, N, P là điểm chính giữa của các cung AB, BC, CA. Gọi D là giao điểm của MN và AB, E là giao điểm của PN và AC. Chứng minh rằng DE song song với BC.
Tam giác ABC nội tiếp đường tròn tâm O, các điểm M, N, P là điểm chính giữa của các cung AB, BC, CA. Gọi D là giao điểm của MN và AB, E là giao điểm của PN và AC. Chứng minh rằng DE song song với BC.
Tam giác ABC nội tiếp đường tròn tâm O, các điểm M, N, P là điểm chính giữa của các cung AB, BC, CA. Gọi D là giao điểm của MN và AB, E là giao điểm của PN và AC. Chứng minh rằng DE song song với BC.
Cho đường tròn O và dây cung BC cố định. Trên cung lớn BC lấy điểm A bất kì (A không trùng với B và C), gọi M, N lần lượt là điểm chính giữa cung BC và cung AB. Gọi I là giao điểm của AM và CN, gọi K là giao điểm của MN với AB
a CM:tứ giác ANKI nội tiếp .
b CM:KI song song với BC
Cho đường tròn (O) và hai dây AB, AC. Gọi M, N lần lượt là điểm chính giữa của cung AB và cung AC. Đường thẳng MN cắt dây AB tại E và cắt dây AC tại H. Chứng minh tam giác AEH là tam giác cân.