Các câu hỏi tương tự
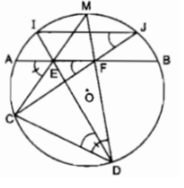
Cho đường tròn tâm O bán kính R và dây AB bất kỳ. Gọi M là điểm chính giữa của cung nhỏ AB. E và F là hai điểm bất kỳ trên dây AB. Gọi C và D tương ứng là giao điểm của ME, MF của đường tròn (O). Chứng minh ∠ EFD + ∠ ECD = 180 °
Cho đường tròn ( O;R ) và dây CD cố định . Trên tia đối CD lấy điểm M . Qua M kẻ 2 tiếp tuyến MA và MB tới đường tròn ( A,B là tiếp điểm, A thuộc cung lớn CD . Gọi I là trung điểm của CD.a ) chứng minh MA^2 MC*MD b) gọi H,P lần lượt là giao điểm của AB với MO,CD . Chứng minh tứ giác OHPI nội tiếp .c) chứng minh tam giác MHC đồng dạng với tam giác MDO và MC*PDMD*PCd) kẻ dây DE của đường tròn ( O,R ) sao cho DE song song AB . Chứng minh C,H,E thẳng hàng .
Đọc tiếp
Cho đường tròn ( O;R ) và dây CD cố định . Trên tia đối CD lấy điểm M . Qua M kẻ 2 tiếp tuyến MA và MB tới đường tròn ( A,B là tiếp điểm, A thuộc cung lớn CD . Gọi I là trung điểm của CD.
a ) chứng minh MA^2 = MC*MD
b) gọi H,P lần lượt là giao điểm của AB với MO,CD . Chứng minh tứ giác OHPI nội tiếp .
c) chứng minh tam giác MHC đồng dạng với tam giác MDO và MC*PD=MD*PC
d) kẻ dây DE của đường tròn ( O,R ) sao cho DE song song AB . Chứng minh C,H,E thẳng hàng .
Cho đường tròn (O) có các dây cung AB, BC, CA. Gọi M là điểm chính giữa của cung nhỏ AB. Vẽ dây MN song song với BC và gọi s là giao điểm của MN và AC. Chứng minh SM = SC và SN = SA
Cho đường tròn (O;R) đường kính AB. Gọi Ax và By là hai tiếp tuyến của (O); C là một điểm trên đường tròn (O), D là điểm nằm giữa A và O. Đường vuông góc với CD tại C cắt Ax và By lần lượt tại E và F.a. Chứng minh: Tứ giác AECD nội tiếp.b. Gọi M là giao điểm của AC và DE, N là giao điểm của BC và DF. Chứng minh: MN song song với AB.c. Tính tổng diện tích hai hình viên phân giới hạn bởi các cung nhỏ AC và BC với các dây AC và BC của (O) khi ACR?
Đọc tiếp
Cho đường tròn (O;R) đường kính AB. Gọi Ax và By là hai tiếp tuyến của (O); C là một điểm trên đường tròn (O), D là điểm nằm giữa A và O. Đường vuông góc với CD tại C cắt Ax và By lần lượt tại E và F.
a. Chứng minh: Tứ giác AECD nội tiếp.
b. Gọi M là giao điểm của AC và DE, N là giao điểm của BC và DF. Chứng minh: MN song song với AB.
c. Tính tổng diện tích hai hình viên phân giới hạn bởi các cung nhỏ AC và BC với các dây AC và BC của (O) khi AC=R?
cho đường tròn tâm O, đường kính AB có dây CD vuông góc với AB.Gọi M là điểm bất kỳ thuộc nửa đường tròn. (MC không song song với AB),E là giao điểm của MD và AB cmr EA/EB=FA/FB
Cho tam giác ABC nhọn nội tiếp trong đường tròn (O). Gọi D là điểm chính giữa của cung nhỏ AB. Vẽ bán kính OE vuông góc với AC. Dây DE cắt AB, AC lần lượt tại H và K.
a) Chứng minh hai góc AHK và AKH bằng nhau
b) Gọi I là giao điểm của BE và CD. Chứng minh CEKI nội tiếp và IK//AB
c) Gọi F là giao điểm của AB và CD. Chứng minh AI.FC<IC.AF+IF.AC
Cho nửa đường tròn tâm O đường kính AB. Gọi C là một điểm trên nửa đường tròn sao cho cung CA nhỏ hơn cung CB. Trên nửa mặt phẳng bờ AB chứa điểm C, kẻ hai tia Ax và By cùng vuông góc với AB.Một đường tròn đi qua A và C (khác với đường tròn đường kính AB) cắt đường kính AB tại D và cắt Ax tại E.đường thẳng EC cắt tia By tại F a) chứng minh BDCF là tứ giác nội tiếp đường trònb) chứng minh CD2 CE.CFc) Gọi I là giao điểm của AC và DE, J là giao điểm của BC và DF. Chứng minh IJ song song với AB d) K...
Đọc tiếp
Cho nửa đường tròn tâm O đường kính AB. Gọi C là một điểm trên nửa đường tròn sao cho cung CA nhỏ hơn cung CB. Trên nửa mặt phẳng bờ AB chứa điểm C, kẻ hai tia Ax và By cùng vuông góc với AB.Một đường tròn đi qua A và C (khác với đường tròn đường kính AB) cắt đường kính AB tại D và cắt Ax tại E.đường thẳng EC cắt tia By tại F
a) chứng minh BDCF là tứ giác nội tiếp đường tròn
b) chứng minh CD2 =CE.CF
c) Gọi I là giao điểm của AC và DE, J là giao điểm của BC và DF. Chứng minh IJ song song với AB
d) Khi EF là tiếp tuyến của nửa đường tròn đường kính AB thì D nằm ở vị trí nào trên AB
cho đường tròn tâm O đường kính AB. Qua trung điểm E của OB, kẻ một dường thẳng vuông góc OB, cắt đường tròn O ở M và N. Kẻ dây MP song song AB. Gọi I là điểm chính giữa của cung nhỏ PM. K là giao điểm của OI và PM. CM: KE song song PN
cho tam giác ABC nội tiếp (O) bán kính R(AB<AC) đường tròn tâm I đường kính OA cắt AB, AC lần lượt tại M và N.và M, N lần lượt là trung điểm AB, AC. Kẻ dây cung AE của (I) đường kính OA song song với MN,.Gọi F là giao điểm của MN và HE.chứng minh F là trung điểm NM