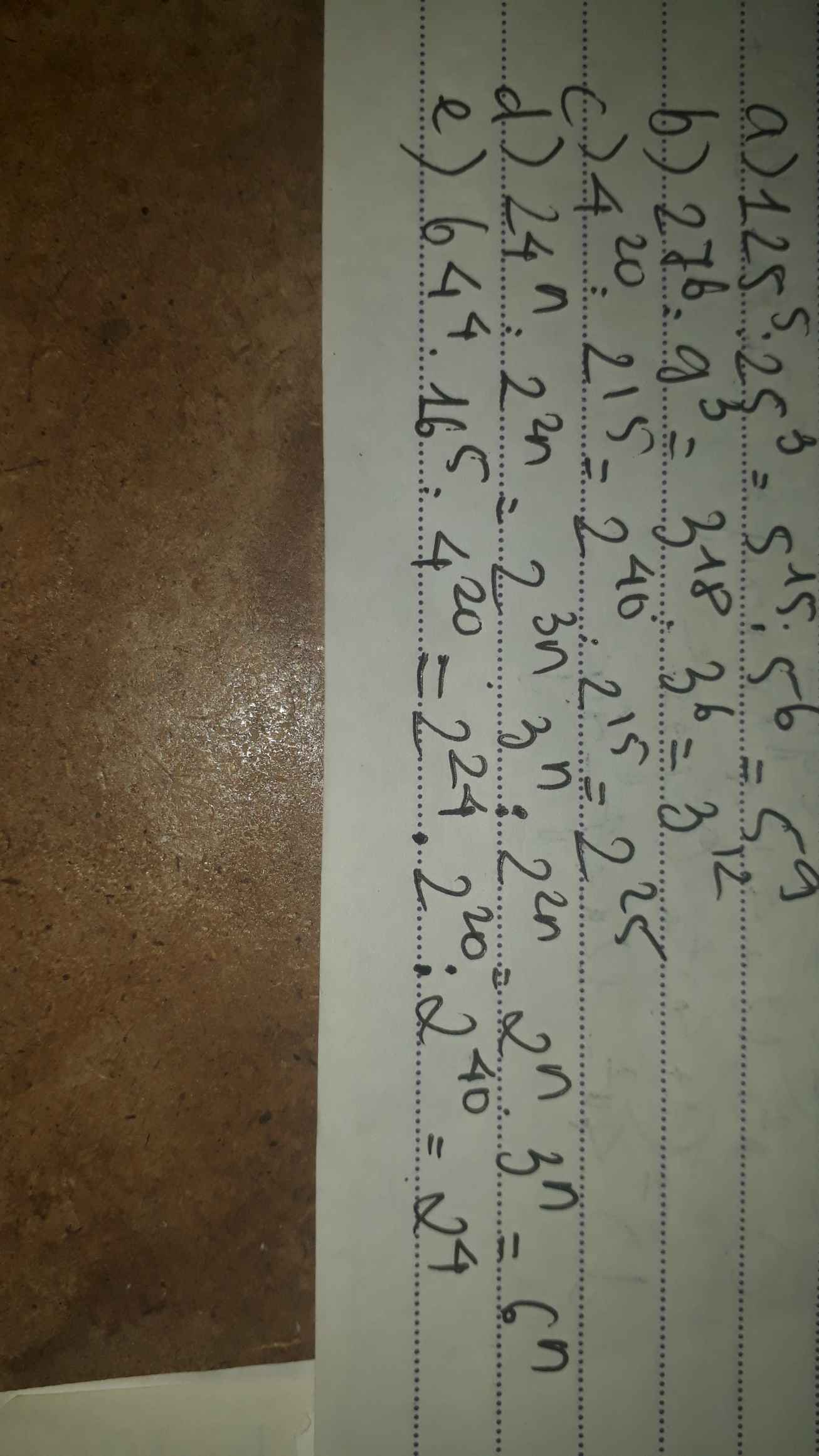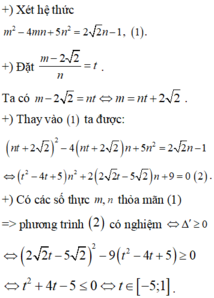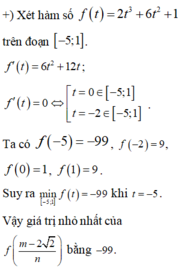24n:22n
Những câu hỏi liên quan
26 tháng 9 2021 lúc 10:56
Viết kết quả sau dưới dạng lũy thừa 24n:22n
\(=\left(4\cdot6\right)^n:\left(2^2\right)^n=4^n\cdot6^n:4^n=6^n\)
Đúng 2
Bình luận (0)
Bài toán 5: Viết các kết quả sau dưới dạng một lũy thừa.
a) 1255: 253 ;b) 276: 93 ; c) 420: 215
d) 24n: 22n ; e) 644. 165: 420
a: \(125^5:25^3=5^{15}:5^6=5^9\)
b: \(27^6:9^3=3^{18}:3^6=3^{12}\)
c: \(4^{20}:2^{15}=2^{40}:2^{15}=2^{45}\)
d: \(24^n:2^{2n}=24^n:4^n=6^n\)
e: \(64^4\cdot16^5:4^{20}=2^{24}\cdot2^{20}:2^{40}=2^4\)
Đúng 1
Bình luận (0)
Cho hai lực đồng quy có độ lớn bằng 16 N và 12 N. Độ lớn và góc hợp bởi hai lực đó là
A. 3N; 30 độ. B. 20N; 90độ. C. 22N; 60độ. D. 24N; 45độ
Ta thử đáp án là cách nhanh nhất nhé!
Thay vào công thức:
\(F=\sqrt{F_1^2+F_2^2+2\cdot F_1\cdot F_2\cdot cos\alpha}\)
Lần lượt thay ta đc đáp án B thỏa man nhé:
\(F=\sqrt{16^2+12^2+2\cdot16\cdot12\cdot cos90^o}=20N\)
Chọn B
Đúng 3
Bình luận (0)
Trong các số sau số nào chia hết cho 2, cho 5, cho 10
a,34n+1+1 (n∈N)
b, 24n+1-2 (n∈N)
c, 22n+4(n∈N,N>2)
d, 94n-6(n∈N,n>1)
Lời giải:
Ta thấy \(2^{4n+2}-2=2(2^{4n}-1)=2(16^n-1)\)
$16\equiv 1\pmod 5\Rightarrow 16^n\equiv 1\pmod 5$
$\Rightarrow 16^n-1\equiv 0\pmod 5$
$\Rightarrow 16^n-1\vdots 5$
$\Rightarrow 2(16^n-1)\vdots 10$
Vậy đáp án b.
Đúng 1
Bình luận (1)
Cho n thuộc N* CMR các số sau là hợp số
a,A = 2^22n+1 + 3
b, B= 2^24n+1 + 7
c, C= 2^26n+2 + 13
Cho mình hỏi một câu hỏi này nhé.
(24n-1) chia hết cho (2983n+1)
(2983n+1) chia hết cho (24n-1)
(2983n+1)khác(24n-1)
Và (24n-1):(2983n+1)=(2983n+1):(24n-1)
Tính n (Những dữ liệu trên đều của 1 bài)
Ai làm đúng và nhanh nhất mình sẽ tick.
CHÚC MỪNG NĂM MỚI !
Cho mình hỏi một câu hỏi này nhé.
(24n-1) chia hết cho (2983n+1)
(2983n+1) chia hết cho (24n-1)
(2983n+1)khác(24n-1)
Và (24n-1):(2983n+1)=(2983n+1):(24n-1)
Tính n (Những dữ liệu trên đều của 1 bài)
Ai làm đúng và nhanh nhất mình sẽ tick.
Chúc các bạn học tốt
CHÚC MỪNG NĂM MỚI !
Xem thêm câu trả lời
Cho hàm số
f
(
x
)
2
x
3
+
6
x
2
+
1
và các số thực m,n thỏa mãn
m
2
-
4
m
n
+
5
n
2
...
Đọc tiếp
Cho hàm số f ( x ) = 2 x 3 + 6 x 2 + 1 và các số thực m,n thỏa mãn m 2 - 4 m n + 5 n 2 = 2 2 n - 1 . Giá trị nhỏ nhất của f m - 2 2 n bằng
A. -99 .
B. -100.
C. 5.
D. 4.
18 tháng 7 2023 lúc 14:24
2n . 22n. 2 3 = 16
`@` `\text {Ans}`
`\downarrow`
\(2^n\cdot2^{2n}\cdot2^3=16\)
`\Rightarrow `\(2^{n+2n+3}=2^4\)
`\Rightarrow `\(2^{3n+3}=2^4\)
`\Rightarrow 3n + 3 = 4`
`\Rightarrow 3n = 4 - 3`
`\Rightarrow 3n = 1`
`\Rightarrow n = `\(\dfrac{1}{3}\)
Vậy, \(n=\dfrac{1}{3}\)
Đúng 2
Bình luận (0)
2n.22n.23 = 16
23n = 16: 23
23n = 2
3n = 1
n = \(\dfrac{1}{3}\)
Đúng 0
Bình luận (0)