Cho x f(x-1) = (x^2 - 4) f(x). CMR : có it nhất 3 giá trị của x để f(x) =0

Những câu hỏi liên quan
cho hàm số y=f(x) thỏa mãn x(f).(x-2)=(x-4).f(x) với mọi giá trị của x. Hãy chứng minh rằng có ít nhất 2 giá trị của x để hàm số có giá trị =0
tick rồi mk giải chi tiết cho
Đúng 0
Bình luận (0)
cho hàm số y=f(x) thỏa mãn x(f).(x-2)=(x-4).f(x) với mọi giá trị của x. Hãy chứng minh rằng có ít nhất 2 giá trị của x để hàm số có giá trị =0
cho hàm số y=f(x) thỏa mãn x(f).(x-2)=(x-4).f(x) với mọi giá trị của x. Hãy chứng minh rằng có ít nhất 2 giá trị của x để hàm số có giá trị =0
tick rồi mk giải chi tiết cho
Đúng 0
Bình luận (0)
1,Tìm các hệ số AB của đa thức f(x) = ax + b, biết : f(1)=1; f(2)=4
2, cho đa thứcf(x) : ax mũ 2 + bx + c = 0 ( vs mọi giá trị x ) . CMR : a=b=c=0
3, Cho đa thức f(x) thỏa mãn, f(x) + x. f(-x) = x+1 vs mọi giá trị của x. Tính f(1)
Cho hàm số y=f(x)=2x^2 -8
a) Tính f(–3) ; f(0) ; f(1) ; f(2) b) Tìm giá trị của x để f(x) có giá trị bằng 0.
a: f(-3)=10
f(0)=-8
f(1)=-6
f(2)=0
b: f(x)=0
=>(x-2)(x+2)=0
=>x=2 hoặc x=-2
Đúng 0
Bình luận (0)
Cho hàm số f(x) có đồ thị của hàm số f(x) như hình vẽ. Biết f(0) + f(1) - 2f(2) f(4) - f(3). Giá trị nhỏ nhất m, giá trị lớn nhất M của hàm số f(x) trên đoạn [0;4] là A. m f(4), M f(1) B. m f(4), M f(2) C. m f(1), M f(2) D. m f(0), M f(2)
Đọc tiếp
Cho hàm số f(x) có đồ thị của hàm số f'(x) như hình vẽ. Biết f(0) + f(1) - 2f(2) = f(4) - f(3). Giá trị nhỏ nhất m, giá trị lớn nhất M của hàm số f(x) trên đoạn [0;4] là
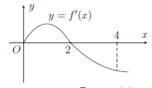
A. m = f(4), M = f(1)
B. m = f(4), M = f(2)
C. m = f(1), M = f(2)
D. m = f(0), M = f(2)
Chọn B
Từ đồ thị của hàm số f'(x) trên đoạn [0;4] ta có bảng biến thiên của hàm số trên đoạn [0;4] như sau:
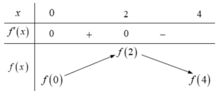
Từ bảng biến thiên ta có ![]()
Mặt khác ![]()
![]()
![]()
![]()
Suy ra ![]()
Đúng 0
Bình luận (0)
Cho hàm số y=f(x) thỏa mãn (x-1).f(x)=[x+4.f(x+8)]. CMR có ít nhất 2 giá trị của x để f(x)=0
\(\left(x-1\right).f\left(x\right)=\left(x+4\right).f\left(x+8\right)\)
+ Thay \(x=1\) vào ta được:
\(\left(1-1\right).f\left(x\right)=\left(1+4\right).f\left(1+8\right)\)
\(\Leftrightarrow5.f\left(9\right)=0\)
\(\Leftrightarrow f\left(9\right)=0:5\)
\(\Rightarrow f\left(9\right)=0.\)
\(\Rightarrow\) \(9\) là nghiệm của \(f\left(x\right).\)
+ Thay \(x=-4\) vào ta được:
\(\left[\left(-4\right)-1\right].f\left(-4\right)=\left[\left(-4\right)+4\right].f\left[\left(-4\right)+8\right]\)
\(\Leftrightarrow-5.f\left(-4\right)=0\)
\(\Leftrightarrow f\left(-4\right)=0:\left(-5\right)\)
\(\Rightarrow f\left(-4\right)=0\)
\(\Rightarrow-4\) là nghiệm của \(f\left(x\right).\)
Vậy \(f\left(x\right)\) có ít nhất hai nghiệm là \(9\) và \(-4.\)
Chúc bạn học tốt!
Cho hàm số y=f(x)=1/2|x|-3
a)Tính f(0); f(-1) ;f(2)
b)Tìm x để f(x)=0
c)Tìm x để f(x)=-2
d)Tìm x để hàm số có giá trị nhỏ nhất
Cho hàm số y=f(x)=1/2|x|-3
a)Tính f(0); f(-1) ;f(2)
b)Tìm x để f(x)=0
c)Tìm x để f(x)=-2
d)Tìm x để hàm số có giá trị nhỏ nhất















