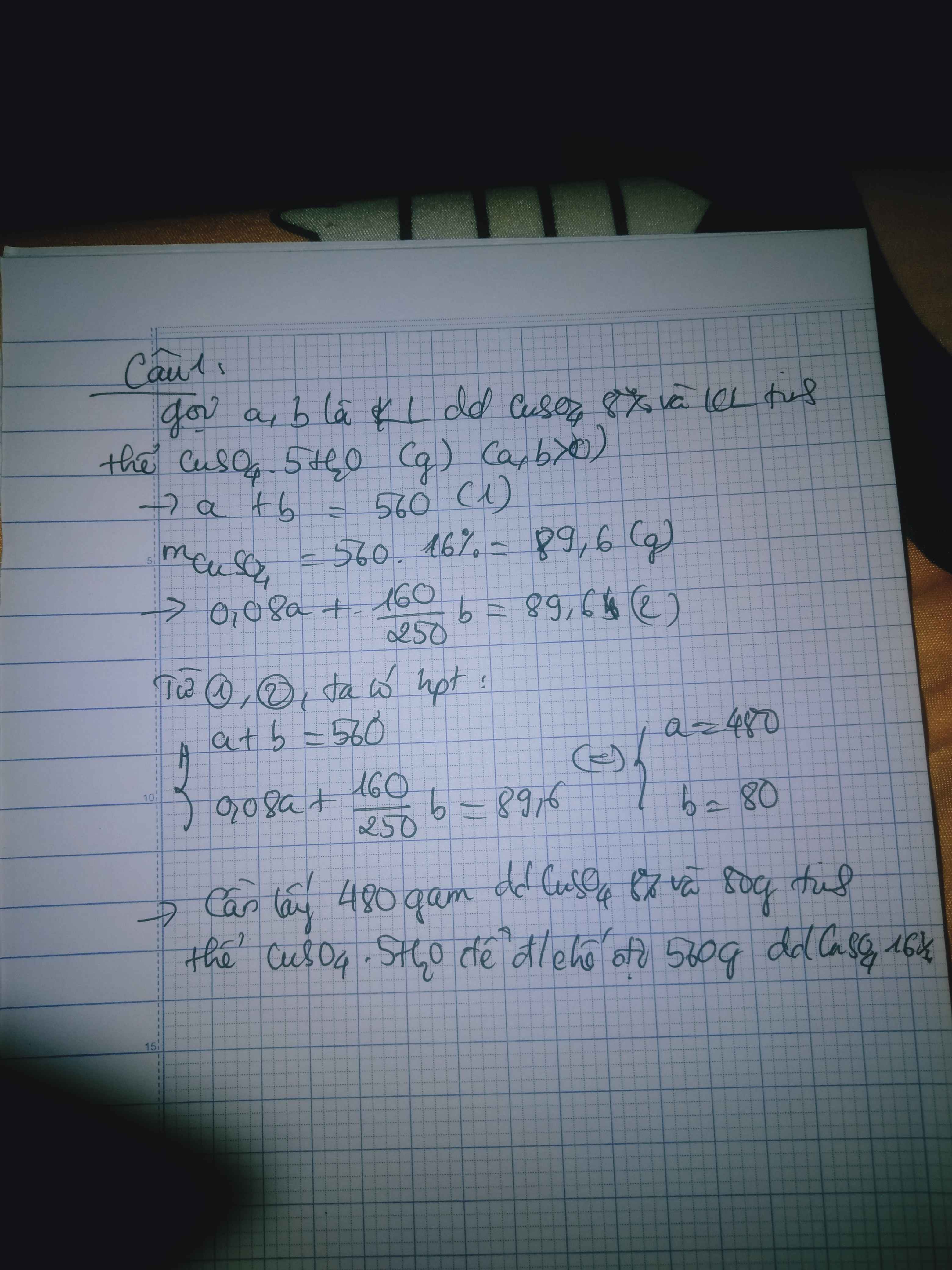Để điều chế 560 g dung dịch CuSO4 16% cần phải lấy bao nhiêu gam dung dịch CuSO4 8%

Những câu hỏi liên quan
Để điều chế 560 g dung dịch CuSO4 16% cần phải lấy bao nhiêu gam dung dịch CuSO4 8% và bao nhiêu gam tinh thể CuSO4.5H2O
Để điều chế 560g dung dịch CuSO4 16% cần phải lấy bao nhiêu gam dung dịch CuSO4 8% trộn với bao nhiêu gam tinh thể CuSO4.5H2O.
\(m_{dd_{CuSO_4}}=a\left(g\right)\)
\(\Rightarrow m_{CuSO_4}=0.08a\left(g\right)\)
\(m_{CuSO_4\cdot5H_2O}=b\left(g\right)\)
\(\Rightarrow m_{CuSO_4}=\dfrac{b}{250}\cdot160=0.64b\left(g\right)\)
\(m_{dd_{CuSO_4\left(15\%\right)}}=a+b=560\left(g\right)\left(1\right)\)
\(m_{CuSO_4\left(15\%\right)}=0.08a+0.64b=560\cdot16\%=89.6\left(g\right)\left(2\right)\)
\(\left(1\right),\left(2\right):a=480,b=80\)
Đúng 5
Bình luận (0)
Gọi $m_{dd\ CuSO_4\ 8\%} = a(gam) ; n_{CuSO_4.5H_2O} = b(mol)$
Sau khi pha :
$m_{CuSO_4} = a.8\% + 160a = 560.16\% = 89,6(gam)$
$m_{dung\ dịch} = a + 250b = 560(gam)$
Suy ra a = 480(gam) ; b = 0,32(mol)$
$m_{CuSO_4.5H_2O} = 0,32.250 = 80(gam)$
Đúng 4
Bình luận (0)
Để pha chế 500g dung dịch CuSO4 16% cần phải lấy bao nhiêu gam dung dịch CuSO4 8% và bao nhiêu gam tinh thể CuSO4 5H2O
mCuSO4=16%.500= 80(g)
Gọi x,y là KL dd CuSO4 8% và tinh thế CuSO4.5H2O cần lấy (x>0)
m(CuSO4)= 0,08x+ 16/25y
<=>0,08x+ 0,64y= 80 (1)
Mặt khác vì KL dung dịch CuSO4 16% là 500 gam nên: x+y=500 (2)
Từ (1), (2) ta có hpt:
\(\left\{{}\begin{matrix}0,08x+0,64y=80\\x+y=500\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3000}{7}\\y=\dfrac{500}{7}\end{matrix}\right.\)
Vậy để pha chế 500 gam dd CuSO4 16% thì cần 3000/7 (g) dd CuSO4 8% và 500/7 (g) tinh thể CuSO4.5H2O.
Đúng 2
Bình luận (1)
Câu 1: Để điều chế 560g dung dịch CuSO4 16% cần phải lấy bao nhiêu gam dung dịch CuSO4 8% và bao nhiêu gam tinh thể CuSO4.5H2O.Câu 2: Cho 200g dung dịch Ba(OH)2 17,1% vào 500g dung dịch hỗn hợp (NH4)2SO4 1,32% và CuSO4 2%. Sau khi kết thúc tất cả các phản ứng ta thu được khí A, kết tủa B và dung dịch C.a/ Tính thể tích khí A (đktc)b/ Lấy kết tủa B rửa sạch và nung ở nhiệt cao đến khối lượng không đổi thì được bao nhiêu gam rắn?c/ Tính nồng độ % của các chất trong C.
Đọc tiếp
Câu 1: Để điều chế 560g dung dịch CuSO4 16% cần phải lấy bao nhiêu gam dung dịch CuSO4 8% và bao nhiêu gam tinh thể CuSO4.5H2O.
Câu 2: Cho 200g dung dịch Ba(OH)2 17,1% vào 500g dung dịch hỗn hợp (NH4)2SO4 1,32% và CuSO4 2%. Sau khi kết thúc tất cả các phản ứng ta thu được khí A, kết tủa B và dung dịch C.
a/ Tính thể tích khí A (đktc)
b/ Lấy kết tủa B rửa sạch và nung ở nhiệt cao đến khối lượng không đổi thì được bao nhiêu gam rắn?
c/ Tính nồng độ % của các chất trong C.
Để điều chế 560g dung dịch CuSO4 15% cần phải lấy bao nhiêu gam dung dịch CuSO4 28% và bao nhiêu gam H2O
\(m_{CuSO_4}=a;m_{H_2O}=b\\ a+b=560\\ C\%_{ddsau}=\dfrac{0,28a}{560}=\dfrac{15}{100}\\ a=300;b=260\)
Vậy cần lấy 300 g dung dịch đồng(II) sulfate 28% pha với 260 g nước.
Đúng 2
Bình luận (0)
cần lấy 300g dung dịch đồng III sulf 28% pha với 160g nước
Đúng 0
Bình luận (0)
Giả sử cần lấy x gam dung dịch CuSO4 28% và y gam H2O để điều chế dung dịch CuSO4 15%.
Theo phần trăm khối lượng, ta có:
Trong x gam dung dịch CuSO4 28%, khối lượng CuSO4 là 0.28x gam.Trong y gam H2O, khối lượng H2O là 0.00y gam.Tổng khối lượng CuSO4 và H2O trong dung dịch CuSO4 15% là 560g, do đó ta có phương trình:
0.28x + 0.00y = 0.15 * 560
Simplifying the equation, we have:
0.28x = 0.15 * 560
0.28x = 84
x = 84 / 0.28
x = 300
Vậy, ta cần lấy 300g dung dịch CuSO4 28% và (560 - 300) = 260g H2O để điều chế dung dịch CuSO4 15%.
Đúng 0
Bình luận (0)
a) Cần lấy bao nhiêu gam tinh thể CuSO4.5H2O và bao nhiêu gam dung dịch CuSO4 8% để điều chế được 280g dung dịch CuSO4 15%
b) Khối lượng riêng của một dung dịch CuSO4 là 1,206 g/ml. Đem cô cạn 414,594 ml dung dịch này thu được 140,625g tinh thể CuSO4.5H2O. Tính nồng độ C% và CM của dung dịch nói trên.
a)
Gọi $n_{CuSO_4.5H_2O} = a(mol) ; m_{dd\ H_2SO_4\ 8\%} = b(gam)$
Sau kho pha :
$m_{dd} = 250a + b = 280(1)$
$m_{CuSO4} = 160a + b.8\% = 280.15\%(2)$
Từ (1)(2) suy ra a = 0,14; b = 245(gam)
$m_{CuSO4.5H_2O} = 0,14.250 = 35(gam)$
Đúng 3
Bình luận (5)
b)
$n_{CuSO_4} = n_{CuSO_4.5H_2O} = \dfrac{140,625}{250} = 0,5625(mol)$
414,594 ml = 0,414594 lít
Suy ra :
$C_{M_{CuSO_4}} = \dfrac{0,5625}{0,414594} = 1,36M$
$m_{dd} = D.V = 1,206.414,594 = 500(gam)$
Suy ra :
$C\%_{CuSO_4} = \dfrac{0,5625.160}{500}.100\% = 18\%$
Đúng 3
Bình luận (0)
cần bao nhiêu gam tinh thể cuso4.5h20 và bao nhiêu gam dung dịch cuso4 8% để điều chế 280 g dung dịch cuso4 16%( làm theo 2 cách
Cần lấy bao nhiêu gam CuSO4.5H2O và bao nhiêu gam dung dịch CuSO4 4% để điều chế 500 gam dung dịch CuSO4 8%
1. Nêu cách phân biệt CaO, MgO, Na2O đều là chất bột màu trắng bằng thuốc thử tự
chọn.
2. Cần lấy bao nhiêu gam tinh thể CuSO4.5H2O và bao nhiêu gam dung dịch CuSO4 4%
để điều chế 500 gam dung dịch CuSO4 8%.
Câu 2.
Gọi \(m_{CuSO_4.5H_2O}=x\left(g\right);m_{CuSO_44\%}=y\left(g\right)\)
\(\Rightarrow x+y=500\left(1\right)\)
Khối lượng \(CuSO_4\) có trong tinh thể \(CuSO_4.5H_2O\) là:
\(m=\dfrac{x}{250}\cdot160=\dfrac{16}{25}x\left(g\right)\)
Khối lượng \(CuSO_4\) có trong \(CuSO_44\%\) là:
\(m=\dfrac{y\cdot4\%}{100\%}=\dfrac{y}{25}\left(g\right)\)
Khối lượng \(CuSO_4\) có trong \(CuSO_48\%\) là:
\(m=\dfrac{500\cdot8\%}{100\%}=40g\)
Bảo toàn cơ năng:
\(\Rightarrow\dfrac{16}{25}x+\dfrac{y}{25}=40\Rightarrow16x+y=1000\left(2\right)\)
Từ (1) và (2)\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{100}{3}\approx33,33g\\y=\dfrac{1400}{3}\approx466,67g\end{matrix}\right.\)
Đúng 2
Bình luận (0)