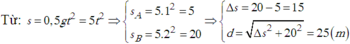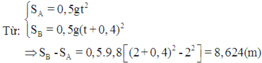Bắt đầu thả rơi tự do (không vận tốc đầu) một viên sỏi lúc tại nơi có gia tốc
. Tốc độ trung bình của viên sỏi trong khoảng thời gian từ
đến
là

Những câu hỏi liên quan
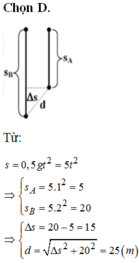
Hai viên bi A và B được thả rơi tự do không vận tốc đầu từ hai điểm cùng một độ cao đủ lớn và cách nhau 20 m. Viên bị A rơi sau viên bi B một khoảng thời gian là 1 s. Tính khoảng cách giữa hai viên bi sau thời gian 2 s kể từ khi B bắt đầu rơi. Lấy gia tốc rơi tự do g 10 m/s2. A. 15 m. B. 32 m. C. 14 m. D. 25 m.
Đọc tiếp
Hai viên bi A và B được thả rơi tự do không vận tốc đầu từ hai điểm cùng một độ cao đủ lớn và cách nhau 20 m. Viên bị A rơi sau viên bi B một khoảng thời gian là 1 s. Tính khoảng cách giữa hai viên bi sau thời gian 2 s kể từ khi B bắt đầu rơi. Lấy gia tốc rơi tự do g = 10 m/s2.
A. 15 m.
B. 32 m.
C. 14 m.
D. 25 m.
Hai viên bi A và B được thả rơi tự do không vận tốc đầu từ hai điểm cùng một độ cao đủ lớn và cách nhau 20 m. Viên bị A rơi sau viên bi B một khoảng thời gian là 1 s. Tính khoảng cách giữa hai viên bi sau thời gian 2 s kể từ khi B bắt đầu rơi. Lấy gia tốc rơi tự do g 10 m/s2. A. 15 m. B. 32 m. C. 14 m. D. 25 m.
Đọc tiếp
Hai viên bi A và B được thả rơi tự do không vận tốc đầu từ hai điểm cùng một độ cao đủ lớn và cách nhau 20 m. Viên bị A rơi sau viên bi B một khoảng thời gian là 1 s. Tính khoảng cách giữa hai viên bi sau thời gian 2 s kể từ khi B bắt đầu rơi. Lấy gia tốc rơi tự do g = 10 m/s2.
A. 15 m.
B. 32 m.
C. 14 m.
D. 25 m.
Hai viên bi A và B được thả rơi tự do không vận tốc ban đầu từ hai điểm cùng một độ cao đủ lớn . Viên bi A rơi sau viên bi B một khoảng thời gian là 0,4 s. Tính khoảng cách giữa hai viên bi theo phương thẳng đứng sau thời gian 2 s kể từ khi bi A bắt đầu rời. Lấy gia tốc rơi tự do g 9,8 m/s2 A. 15 m. B. 11 m. C. 8,624 m. D. 25m.
Đọc tiếp
Hai viên bi A và B được thả rơi tự do không vận tốc ban đầu từ hai điểm cùng một độ cao đủ lớn . Viên bi A rơi sau viên bi B một khoảng thời gian là 0,4 s. Tính khoảng cách giữa hai viên bi theo phương thẳng đứng sau thời gian 2 s kể từ khi bi A bắt đầu rời. Lấy gia tốc rơi tự do g = 9,8 m/s2
A. 15 m.
B. 11 m.
C. 8,624 m.
D. 25m.
Hai viên bi A và B được thả rơi tự do không vận tốc ban đầu từ hai điểm cùng một độ cao đủ lớn. Viên bi A rơi sau viên bi B một khoảng thời gian là 0,4 s. Tính khoảng cách giữa hai viên bi theo phương thẳng đứng sau thời gian 2 s kể từ khi bi A bắt đầu rời. Lấy gia tốc rơi tự do g 9,8 m/
s
2
. A. 15 m. B. 11 m. C. 8,624 m. D. 25m.
Đọc tiếp
Hai viên bi A và B được thả rơi tự do không vận tốc ban đầu từ hai điểm cùng một độ cao đủ lớn. Viên bi A rơi sau viên bi B một khoảng thời gian là 0,4 s. Tính khoảng cách giữa hai viên bi theo phương thẳng đứng sau thời gian 2 s kể từ khi bi A bắt đầu rời. Lấy gia tốc rơi tự do g = 9,8 m/ s 2 .
A. 15 m.
B. 11 m.
C. 8,624 m.
D. 25m.
Hai viên bi A và B được thả rơi tự do từ cùng một độ cao. Viên bi A rơi sau viên bi B một khoảng thời gian là 0,5 s. Tính khoảng cách giữa hai viên bi sau thời gian 2 s kể từ khi bi A bắt đầu rơi. Lấy gia tốc rơi tự do g = 9,8 m/ s 2
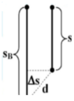
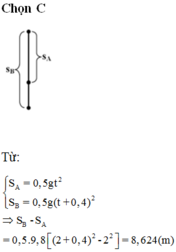
Chọn thời điểm viên bi A bắt đầu rơi làm mốc thời gian. Nếu gọi t là thời gian rơi của viên bi A thì thời gian rơi của viên bi B sẽ là t' = t + 0,5. Như vậy quãng đường mà viên bi A và B đã đi được tính theo các công thức :
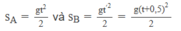
Từ đó suy ra khoảng cách giữa hai viên bi sau khoảng thời gian 2 s kể từ khi bi A bắt đầu rơi
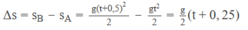
Suy ra ∆ s ≈ 11m
Đúng 1
Bình luận (0)
Một vật được thả rơi tự do không vận tốc từ độ cao h so với mặt đất tại nơi có gia tốc trọng trường g=10m/s². Quãng đường vật rơi trong nửa thời gian sau dài hơn quãng đường vật rơi trong nửa thời gian đầu 40m. Tính h, thời gian rơi và tốc độ của vật khi chạm đất.
\(s_2-s_1=40\Leftrightarrow s-s_1-s_1=40\Leftrightarrow s-2s_1=40\)
\(\Rightarrow\dfrac{1}{2}gt^2-2\cdot\dfrac{1}{2}gt_1^2=40\)
Mà: \(t_1=\dfrac{1}{2}t\Rightarrow\dfrac{1}{2}gt^2-2\cdot\dfrac{1}{2}g\left(\dfrac{1}{2}t\right)^2=40\)
\(\Leftrightarrow\dfrac{1}{4}gt^2=40\Leftrightarrow t=\sqrt{\dfrac{40}{\dfrac{1}{4}g}}=\sqrt{\dfrac{40}{\dfrac{1}{4}\cdot10}}=4\left(s\right)\)
\(\Rightarrow\left\{{}\begin{matrix}h=s=\dfrac{1}{2}gt^2=\dfrac{1}{2}\cdot10\cdot4^2=80\left(m\right)\\v=gt=10\cdot4=40\left(m/s\right)\end{matrix}\right.\)
Vậy: h = 80 (m), t = 4 (s) và v = 40 (m/s).
Đúng 0
Bình luận (0)
Một vật được thả rơi tự do không vận tốc đầu từ độ cao h so với mặt đất tại nơi có gia tốc trọng trường g = 10 m / s 2 . Quãng đường vật rơi trong nửa thời gian sau dài hơn quãng đường vật rơi trong nửa thời gian đầu 40m. Tính độ cao h và tốc độ của vật khi chạm đất.
Một vật được thả rơi tự do không vận tốc đầu từ độ cao h so với mặt đất tại nơi có gia tốc trọng trường g=10m/ s 2 . Quãng đường vật rơi trong nửa thời gian sau dài hơn quãng đường vật rơi trong nửa thời gian đầu 40m. Tính độ cao h và tốc độ của vật khi chạm đất.
Quãng đường vật rơi nửa thời gian đầu:
![]()
Quãng đường vật rơi nửa thời gian cuối
![]()
Quãng đường vật rơi: h = h 1 + h 2
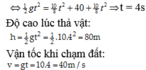
Đúng 0
Bình luận (0)
Một vật được thả rơi tự do không vận tốc đầu từ độ cao h so với mặt đất tại nơi có gia tốc trọng trường g
10
m
/
s
2
. Quãng đường vật rơi trong nửa thời gian sau dài hơn quãng đường vật rơi trong nửa thời gian đầu 40m. Tính độ cao h và tốc độ của vật khi chạm đất. A. 70m; 40m/s B. 80m; 50m/s C. 70m; 40m/s D. 80m; 40m/s
Đọc tiếp
Một vật được thả rơi tự do không vận tốc đầu từ độ cao h so với mặt đất tại nơi có gia tốc trọng trường g = 10 m / s 2 . Quãng đường vật rơi trong nửa thời gian sau dài hơn quãng đường vật rơi trong nửa thời gian đầu 40m. Tính độ cao h và tốc độ của vật khi chạm đất.
A. 70m; 40m/s
B. 80m; 50m/s
C. 70m; 40m/s
D. 80m; 40m/s
Đáp án D
Quãng đường vật rơi nửa thời gian đầu:
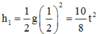
Quãng đường vật rơi nửa thời gian cuối
![]()
Quãng đường vật rơi:
![]()
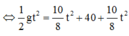
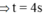
Độ cao lúc thả vật:
![]()
Vận tốc khi chạm đất:
v = gt = 10.4 = 40m/s
Đúng 0
Bình luận (0)