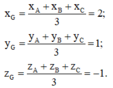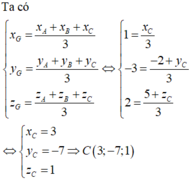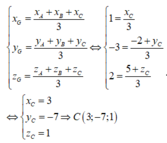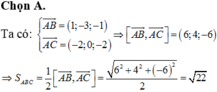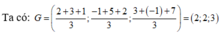Trong không gian với hệ tọa độ Oxyz cho tam giác ABC có A(1;0;0), B(0; -2;3), C(1;1;1). Phương trình mặt phẳng (P) chứa A, B sao cho khoảng cách từ C tới (P) là \(\dfrac{2}{\sqrt{3}}\)

Những câu hỏi liên quan
Trong không gian với hệ tọa độ Oxyz cho tam giác ABC có
A
(
1
;
−
1
;
0
)
,
B
(
2
;
3
;
1
)
,
C
(
3
;
1
;
−
4
)
. Tọa độ tâm G của tam giác ABC là A. G(6;3;-3) B. G(4;2;-2) C. G(-2;-1;1) D. G(2;1;-1)
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho tam giác ABC có A ( 1 ; − 1 ; 0 ) , B ( 2 ; 3 ; 1 ) , C ( 3 ; 1 ; − 4 ) . Tọa độ tâm G của tam giác ABC là
A. G(6;3;-3)
B. G(4;2;-2)
C. G(-2;-1;1)
D. G(2;1;-1)
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A(1;2;-1), B(2;-1;3), C(-4;7;5). Tọa độ chân đường phân giác trong góc
B
^
của tam giác ABC là A.
-
2
3
;
11
3
;...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A(1;2;-1), B(2;-1;3), C(-4;7;5). Tọa độ chân đường phân giác trong góc B ^ của tam giác ABC là
A. - 2 3 ; 11 3 ; 1
B. 11 3 ; - 2 ; 1
C. 2 3 ; 11 3 ; 1 3
D. (-2;11;1)
Đáp án A
Gọi D là chân đường phân giác góc B của tam giác ABC . Theo tính chất đường phân giác ta có : 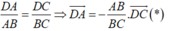
![]()
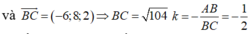
Từ (*) ta có, điểm D chia đoạn thẳng AC theo tỷ số k nên D có toạ độ
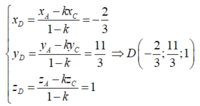
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho tam giác
A
B
C
c
ó
A
(
1
;
−
2
;
3
)
,
B
(
−
1
;
0
;
2
)
v
à
G
(
1
;
−
3
;
2
)
là trọng tâm tam giác ABC. Tìm tọa độ đi...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho tam giác A B C c ó A ( 1 ; − 2 ; 3 ) , B ( − 1 ; 0 ; 2 ) v à G ( 1 ; − 3 ; 2 ) là trọng tâm tam giác ABC. Tìm tọa độ điểm C
A. C ( 3 ; − 7 ; 1 )
B. C ( 2 ; − 4 ; − 1 )
C. C ( 1 ; − 1 ; − 3 )
D. C ( 3 ; 2 ; 1 )
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A(1;-2;3); B(-1;0;2) và G(1;-3;2) là trọng tâm tam giác ABC. Tìm tọa độ điểm C.
A. C(3;2;1)
B. C(2;-4;-1)
C. C(1;-1;-3)
D. C(3;-7;1)
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A (1;-2;3), B (-1;0;2) và G (1;-3;2) là trọng tâm tam giác ABC. Tìm tọa độ điểm C.
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho tam
giác ABC có A (1;-2;3), B (-1;0;2) và G (1;-3;2)
là trọng tâm tam giác ABC. Tìm tọa độ điểm C.
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A(0;1;1), B(1;-2;0), C(-2;1;-1). Diện tích tam giác ABC là
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A(0;1;1), B(1;-2;0), C(-2;1;-1). Diện tích tam giác ABC là
![]()
![]()
![]()
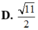
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có
A
2
;
−
1
;
3
,
B
3
;
5
;
−
1
và
C
1
;
2
;
7...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A 2 ; − 1 ; 3 , B 3 ; 5 ; − 1 và C 1 ; 2 ; 7 . Tìm tọa độ trọng tâm G của tam giác ABC
A. G 2 ; 2 ; 3
B. G 6 ; 6 ; 9
C. G 4 3 ; 7 3 ; 10 3
D. G 3 ; 3 ; 9 2
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có
A
2
;
−
1
;
3
,
B
3
;
5
;
−
1
và
C
1
;
2
;
7...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A 2 ; − 1 ; 3 , B 3 ; 5 ; − 1 và C 1 ; 2 ; 7 . Tìm tọa độ trọng tâm G của tam giác ABC
A. G 2 ; 2 ; 3
B. G 6 ; 6 ; 9
C. G 4 3 ; 7 3 ; 10 3
D. G 3 ; 3 ; 9 2
Đáp án A.
Ta có:
G = 2 + 3 + 1 3 ; − 1 + 5 + 2 3 ; 3 + − 1 + 7 3 = 2 ; 2 ; 3 .
Chú ý: Trong không gian Oxyz, cho tam giác ABC. Khi đó trọng tâm G của tam giác có tọa độ là x A + x B + x C 3 ; y A + y B + y C 3 ; z A + z B + z C 3
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có
A
1
;
2
;
−
1
,
B
2
;
−
1
;
3
,
C
−
4
;
7
;...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A 1 ; 2 ; − 1 , B 2 ; − 1 ; 3 , C − 4 ; 7 ; 5 . Tọa độ chân đường phân giác trong góc B ^ của tam giác ABC là
A. − 2 3 ; 11 3 ; 1
B. 11 3 ; − 2 ; 1
C. 2 3 ; 11 3 ; 1 3
D. − 2 ; 11 ; 1
Đáp án A
Gọi D là chân đường phân giác góc B của Δ A B C . Theo tính chất đường phân giác ta có : D A A B = D C B C ⇒ D A → = − A B B C . D C → *
Với A B → = 1 ; − 3 ; 4 ⇒ A B = 26 và B C → = − 6 ; 8 ; 2 ⇒ B C = 104
k = − A B B C = − 1 2
Từ (*) ta có, điểm D chia đoạn thẳng AC theo tỷ số k nên D có toạ độ x D = x A − k x C 1 − k = − 2 3 y D = y A − k y C 1 − k = 11 3 z D = z A − k z C 1 − k = 1 ⇒ D − 2 3 ; 11 3 ; 1
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A(3;0;0), B(0;3;0) và C(0;0;3). Tìm tọa độ trọng tâm G của tam giác ABC. A. G(3;3;3) B. G(1;1;1) C. G(2/3;2/3;2/3) D. G(1/3;1/3;1/3).
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A(3;0;0), B(0;3;0) và C(0;0;3). Tìm tọa độ trọng tâm G của tam giác ABC.
A. G(3;3;3)
B. G(1;1;1)
C. G(2/3;2/3;2/3)
D. G(1/3;1/3;1/3).
Đáp án B
Tọa độ trọng tâm tam giác ABC là G(1;1;1).
Đúng 0
Bình luận (0)