Do x+ y= 1 nên

S = 16 x 2 y 2 + 12 ( x + y ) ( x 2 - x y + y 2 ) + 34 x y = 16 x 2 y 2 + 12 ( x + y ) 2 - 3 x y + 34 x y ,   d o   x + y = 1 = 16 x 2 y 2 - 2 x y + 12

Đặt t= xy . Do x≥ 0 ; y≥0  nên

  0 ≤ x y ≤ ( x + y ) 2 4 = 1 4 ⇒ t ∈ 0 ; 1 4

Xét hàm số f(t) = 16t²- 2t + 12  trên [0 ; 1/4].

Ta có f’ (t) = 32t- 2 ; f’(t) =0 khi t= 1/ 16  .

Bảng biến thiên

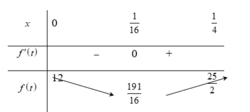
Từ bảng biến thiên ta có:

m i n 0 ; 1 4 f ( t ) = f ( 1 16 ) = 191 16 ;         m a x 0 ; 1 4 f ( t ) = f ( 1 4 ) = 25 2

Vậy giá trị lớn nhất của S là 25/2 đạt được khi 

x + y = 1 x y = 1 4 ⇔ x = 1 2 y = 1 2

giá trị nhỏ nhất của S  là 191/ 16 đạt được khi

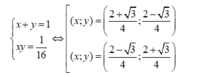
Chọn A.

Đáp án B.

Ta có \(\sqrt{8a^2+56}=\sqrt{8\left(a^2+7\right)}=2\sqrt{2\left(a^2+ab+2bc+2ca\right)}\)

\(=2\sqrt{2\left(a+b\right)\left(a+2c\right)}\le2\left(a+b\right)+\left(a+2c\right)=3a+2b+2c\)

Tương tự \(\sqrt{8b^2+56}\le2a+3b+2c;\)\(\sqrt{4c^2+7}=\sqrt{\left(a+2c\right)\left(b+2c\right)}\le\frac{a+b+4c}{2}\)

Do vậy \(Q\ge\frac{11a+11b+12c}{3a+2b+2c+2a+3b+2c+\frac{a+b+4c}{2}}=2\)

Dấu "=" xảy ra khi và chỉ khi \(\left(a,b,c\right)=\left(1;1;\frac{3}{2}\right)\)

a) \(P=1957\)

b) \(S=19.\)

\(P-\dfrac{5}{2}=x+2y-\dfrac{x^2+y^2}{2}=-\dfrac{1}{2}\left(x-1\right)^2-\dfrac{1}{2}\left(y-2\right)^2+\dfrac{5}{2}\le\dfrac{5}{2}\)

\(\Rightarrow P-\dfrac{5}{2}\le\dfrac{5}{2}\Rightarrow P\le5\)

\(P_{max}=5\) khi \(\left(x;y\right)=\left(1;2\right)\)

Ta có 

A = a⁶ + b⁶ = (a² + b²)(a⁴ - a² b² + b⁴)

= a⁴ - a² b² + b⁴ = (a² + b²)² - 3a²b² = 1 - 3a² b² (1)

Ta lại có

1 = a² + b² \(\ge\)2ab

\(\Rightarrow ab\le\frac{1}{2}\)(2)

Từ (1) và (2) =>A \(\ge1-\frac{3}{4}=\frac{1}{4}\)

Đạt được khi a² = b² = 0,5

Giá trị lớn nhất không có

Ta có a3+b3=(a+b)(a2−ab+b2)=a2−ab+b2a3+b3=(a+b)(a2−ab+b2)=a2−ab+b2 ( vì a+b=1)

Lại có 2(a−b)2≥0⇔2a2−4ab+2b2≥0⇔4a2−4ab+4b2≥2a2+2b2⇔4(a2−ab+b2)≥2(a2+b2)≥(a+b)2=1⇔4(a2−ab+b2)≥1⇔a2−ab+b2≥14⇒a3+b3≥142(a−b)2≥0⇔2a2−4ab+2b2≥0⇔4a2−4ab+4b2≥2a2+2b2⇔4(a2−ab+b2)≥2(a2+b2)≥(a+b)2=1⇔4(a2−ab+b2)≥1⇔a2−ab+b2≥14⇒a3+b3≥14

Vậy Min M=14⇔a=b=12

Ta có : M = a³ + b³ + ab

= ( a + b ) ( a² - ab + b² ) + ab = a² + b²

a + b = 1 \(\Rightarrow\)a² + 2ab + b² = 1   ( 1 ) 

mặt khác : ( a - b )²  \(\ge\)0 \(\Rightarrow\)a² - 2ab + b² \(\ge\)0   ( 2 )

Cộng ( 1 ) với ( 2 ), ta được 2 ( x² + y² ) \(\ge\)1 \(\Rightarrow\)( x² + y² ) \(\ge\)\(\frac{1}{2}\)

\(\Rightarrow\)giá trị nhỏ nhất của M = \(\frac{1}{2}\) \(\Leftrightarrow\)x = y = \(\frac{1}{2}\)

Phan Việt Anh bạn làm đúng đề k vậy 
a^3+b^3+ab mà bạn

Đáp án C

Ta có: 2 x + 1 4 y 2 x + y ≥ 2 + 1 2 2  (Bất đẳng thức Bunhia Scopky).

(ngoài ra các em có thể thế và xét hàm).

Do đó P ≥ 5.

Đáp án C

Áp dụng bất đẳng thức Bunhiacopxki,

ta có  2 x + 1 4 y 2 x + y ≥ 2 + 1 2 2 ⇒ P ≥ 5