tìm hai số nguyên dương a và b biết :
a+3^b=138
Tìm số nguyên dương a và b biết: 27a + 3^b = 138
Nếu b=1 => a=3
Nếu b>=2 thì 3^b chia hết cho 9 => VT chia hết cho 9
Mà 138 = VP ko chia hết cho 9
=> ko tồn tại a,b với b>2
Vậy a=5;b=1
k mk nha
a) Tìm số a,b,c biết 4a=3b;5=7b và 3a+4b-2c=138
b) Tìm cặp x;y nguyên dương biết /x+/y=1/3
1/ a)Cho A= 20+21+22+23+24+25 +26 .........+ 299 CMR: A chia hết cho 31
b)tìm số tự nhiên n để 3n+4 chia hết cho n -1
2/tìm hai số nguyên dương a, b biết [ a,b] = 240 và (a,b) = 16
3/tìm hai số nguyên dương a,b biết rằng ab=216 và (a ,b)=6
4/tìm hai số nguyên dương a,b biết rằng ab=180 , [a,b] =60
5/tìm hai số nguyên dương a,b biết a/b =2,6 và (a,b) =5
6/ tìm a,b biết a/b=4/5 và [ a,b ] = 140
7/tìm số nguyên dương a,b biết a+b = 128 và (a ,b)=16
8/ a)tìm a,b biết a+b = 42 và [a,b] = 72
b)tìm a,b biết a-b =7 , [a,b] =140
9/tìm hai số tự nhiên , biết rằng tổng cúa chúng bằng 100 và có UwCLN là 10
10/ tìm 2 số tự nhiên biết ƯCLN của chúng là 5 và chúng có tích là 300
11/ chứng minh rằng nếu số nguyên tố p> 3 thì (p - 1) . (p + 1) chia hết cho 24
12/ tìm hai số tự nhiên a,b (a < b ) biết ƯCLN (a,b ) = 12 , BCNN(a,b) = 180
BÀI NÀY Ở ĐÂU MÀ NHIỀU THẾ BẠN!?
GIẢI CHẮC ĐÃ LẮM ĐÓ
câu 1 a) thíu là chứng minh rằng a chia hết cho 31
Tìm hai số nguyên dương a và b biết a+2 chia hết cho b và b+3 chia hết cho a?
Bài1
a)Tim hai số nguyên dương a va b biết
a.b=216va UWCLN(a,b)=6
b)Tìm hai số nguyên dương a và b biết tích
a.b=180 và BCNN(a,b)=60
c)tìm a và b biết
a\b=2,6va UWCLN(a,b)=5
Tìm hai số nguyên dương a,b biết: [a,b]=900 và (a,b)=10
Tìm hai số nguyên dương a,b biết: [a,b] = 336 và (a,b) = 12
Ta có: a.b = BCNN(a,b).ƯCLN(a,b) = 336.12 = 4032.
Vì ƯCLN(a,b) = 12 => a = 12a’, b = 12b’ (a’, b’N), ƯCLN(a’,b’) = 1
=>12a’.12b’ = 4032 => a’b’ = 4032:(12.12) = 28
Do a’ > b’ và ƯCLN(a’,b’) = 1 nên ta có:
Với: a’ = 28, b’ = 1 => a = 336 ; b = 12.
Với: a’ = 7, b = 4 => a = 84, b = 48
Tìm hai số nguyên dương a,b biết: [a,b] = 900 và (a,b) = 10
Vì (a,b) = 10 nên a = 10x, b = 10y, với (x,y)=1
Suy ra a.b=10x.10y = 100xy.
Lại có a.b = [a,b].(a,b) = 900.10 = 9000
Suy ra 100xy = 9000 => xy = 90
Giả sử x<y và (x,y)=1 ta có các trường hợp sau:
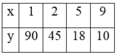
Từ đó suy ra a,b có các trường hợp sau:
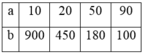
Tìm hai số nguyên dương a, b biết: a , b = 336 và a , b = 12 .