một vật trượt không vận tốc ban đầu trên mặt phẳng nghiêng từ độ cao h và dừng lại ở khoảng cách s theo phương ngang chứng minh rằng hệ số ma sát =h/s xem răng hệ số ma sát như nhau trên mặt phẳng nghiêng và ngang

Những câu hỏi liên quan
: Mặt phẳng nghiêng hợp với phương ngang một góc
α
30
0
, tiếp theo là mặt phẳng nằm ngang như hình vẽ. một vật trượt không vận tốc ban đầu từ đỉnh A của mặt phăng nghiêng với độ cao h1m và sau đó tiếp tục trượt trên mặt phẳng nằn ngang một khoảng là BC. Tính BC, biết hệ số ma sát giữa vật với hai mặt phẳng đều là
μ
0
,
1
Đọc tiếp
: Mặt phẳng nghiêng hợp với phương ngang một góc α = 30 0 , tiếp theo là mặt phẳng nằm ngang như hình vẽ. một vật trượt không vận tốc ban đầu từ đỉnh A của mặt phăng nghiêng với độ cao h=1m và sau đó tiếp tục trượt trên mặt phẳng nằn ngang một khoảng là BC. Tính BC, biết hệ số ma sát giữa vật với hai mặt phẳng đều là μ = 0 , 1
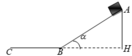
Chọn mốc thế năng tại mặt nằm ngang BC
Theo định luật bảo toàn năng lượng
W A = W C + A m s
Mà W A = m g . A H = m .10 = 10. m ( J ) ; W C = 0 ( J ) A m s = μ m g cos α . A B + μ m g . B C = 0 , 1. m .10. cos 30 0 . A H sin 30 0 + 0 , 1. m .10. B C ⇒ A m s = m . 3 . + m . B C ⇒ 10. m = 0 + m 3 + m . B C ⇒ B C = 8 , 268 ( m )
Đúng 0
Bình luận (0)
Một vật trượt với vận tốc đầu 18 km/h xuống mặt phẳng nghiêng, vật trược nhanh dần đều với gia tốc 1.5 m/s^2. Dến mặt phẳng nghiêng đạt vận tốc 13 m/s và tiếp tục trượt trên mặt phẳng ngang. Hệ số ma sát trên mặt phẳng ngang là 0.2. Mặt phẳng nghiêng hợp với mặt phẳng ngang góc alpha30^0 . Cho g10m/s2.
a. Tìm hệ số ma sát trên mặt phẳng nghiêng.
b. Tìm chiều dài mặt phẳng nghiêng.
c. Tính thời gian từ lúc vật bắt đầu trượt xuống mặt phẳng nghiêng đến lúc dừng lại
Đọc tiếp
Một vật trượt với vận tốc đầu 18 km/h xuống mặt phẳng nghiêng, vật trược nhanh dần đều với gia tốc 1.5 m/\(s^2\). Dến mặt phẳng nghiêng đạt vận tốc 13 m/s và tiếp tục trượt trên mặt phẳng ngang. Hệ số ma sát trên mặt phẳng ngang là 0.2. Mặt phẳng nghiêng hợp với mặt phẳng ngang góc \(\alpha=30^0\) . Cho g=10m/s2.
a. Tìm hệ số ma sát trên mặt phẳng nghiêng.
b. Tìm chiều dài mặt phẳng nghiêng.
c. Tính thời gian từ lúc vật bắt đầu trượt xuống mặt phẳng nghiêng đến lúc dừng lại
Một vật trượt không vận tốc đầu từ đỉnh một mặt phẳng nghiêng xuống mặt phẳng nằm ngang. Vật chuyển động trên mặt phẳng nằm ngang được 3,2m thì dừng lại. Ma sát trên mặt phẳng nghiêng không đáng kể, hệ số ma sát trên mặt phẳng nằm ngang là 0,25. Lấy g=10m/s2
a. Tính vận tốc tại chân mặt phẳng nghiêng
b. Tính độ cao mặt phẳng nghiêng
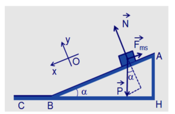
Một mặt phẳng AB nghiêng một góc 300 so với mặt phẳng ngang BC. Biết AB 1m, BC 10,35m, hệ số ma sát trên mặt phẵng nghiêng m1 0,1. Lấy g 10m/s2. Một vật khối lượng m 1kg trượt không có vận tốc ban đầu từ đỉnh A tới C thì dừng lại. Tính vận tốc của vật tại B và hệ số ma sát m2 trên mặt phẳng ngang.
A
.
v
2
2
m
/
s
;
μ...
Đọc tiếp
Một mặt phẳng AB nghiêng một góc 300 so với mặt phẳng ngang BC. Biết AB = 1m, BC = 10,35m, hệ số ma sát trên mặt phẵng nghiêng m1 = 0,1. Lấy g = 10m/s2. Một vật khối lượng m = 1kg trượt không có vận tốc ban đầu từ đỉnh A tới C thì dừng lại. Tính vận tốc của vật tại B và hệ số ma sát m2 trên mặt phẳng ngang.
A . v = 2 2 m / s ; μ = 0 , 04
B . v = 2 m / s ; μ = 0 , 02
C . v = 2 3 m / s ; μ = 0 , 03
D . v = 2 5 m / s ; μ = 0 , 05
Đáp án: A
Phương trình động lực học:
![]()
Chiếu (1) lên phương song song với mặt phẵng nghiêng (phương chuyển động), chiều dương hướng xuống (cùng chiều chuyển động), ta có:
Psina – Fms = ma1
Chiếu (1) lên phương vuông góc với mặt phẵng nghiêng (vuông góc với phương chuyển động), chiều dương hướng lên, ta có:
N - Pcosa = 0
→ N = Pcosa = mgcosa
→ Fms = m1N = m1mgcosa.
Gia tốc trên mặt phẵng nghiêng:
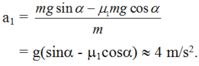
Vận tốc của vật tại B:
![]()
Gia tốc của vật trên mặt phẵng ngang:
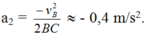
Trên mặt phẵng ngang ta có:
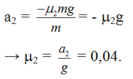
Đúng 0
Bình luận (0)
Từ mặt phẳng nghiêng 30° so với phương ngang, vật có khối lượng 1 kg được truyền vận tốc ban đầu 10m/s song song với mặt phẳng nghiêng. Nó trượt lên trên mặt phẳng hệ số ma sát 0,1. a/ vật lên tới điểm có độ cao bao nhiêu thì dừng lại? b/ Tính công của trọng lực, công của lực ma sát khi vật đi từ chân lên đỉnh dốc nghiêng.
một vật có khối lượng 200g trượt không vận tốc ban đầu từ đỉnh một mặt phẳng nghiêng dài 8m nghiêng góc anpha=30độ so với phương ngang . Lấy g=10m/s ma sát giữa vật và mặt phẳng nghiêng rất nhỏ .Sau khi trượt xuống chân mặt phẳng nghiêng vật tiếp tục trượt trên mặt phẳng ngang với hệ số ma sát trượt là vuy=0.2 . Hãy tính thời gian vật chuyển động trên mặt phẳng ngang
200g=0,2kg
các lực tác dụng lên vật khi ở trên mặt phẳng nghiêng
\(\overrightarrow{P}+\overrightarrow{N}=m.\overrightarrow{a}\)
chiếu lên trục Ox có phương song song với mặt phẳng nghiêng, chiều dương cùng chiều chuyển động
P.sin\(\alpha\)=m.a\(\Rightarrow\)a=5m/s2
vận tốc vật khi xuống tới chân dốc
v2-v02=2as\(\Rightarrow\)v=\(4\sqrt{5}\)m/s
khi xuống chân dốc trượt trên mặt phẳng ngang xuất hiện ma sát
các lực tác dụng lên vật lúc này
\(\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{F_{ms}}=m.\overrightarrow{a'}\)
chiếu lên trục Ox có phương nằm ngang chiều dương cùng chiều chuyển động của vật
-Fms=m.a'\(\Rightarrow-\mu.N=m.a'\) (1)
chiếu lên trục Oy có phương thẳng đứng chiều dương hướng lên trên
N=P=m.g (2)
từ (1),(2)\(\Rightarrow\)a'=-2m/s2
thời gian vật chuyển động trên mặt phẳng đến khi dừng lại là (v1=0)
t=\(\dfrac{v_1-v}{a'}\)=\(2\sqrt{5}s\)
Đúng 1
Bình luận (2)
Một mặt phẳng AB nghiêng một góc 300 so với mặt phẳng ngang BC Biết AB =1m BC = 10,35 , hệ số ma sát trên mặt phẳng nghiêng là k1=0,1 lấy g =10m/s2. Một vật khối lượng m =1kg trượt không có vận tốc ban đầu từ đỉnh A tới C thì dừng lại. Tính vận tốc của vật tại B và hệ số ma sát k2 trên mặt phẳng ngang
theo định luật II niu tơn trên mặt phẳng nghiêng AB
\(\overrightarrow{F_{ms}}+\overrightarrow{N}+\overrightarrow{P}=m.\overrightarrow{a}\) (1)
chiếu (1) lên trục Ox phương song song với mặt phẳng nằm nghiêng chiều dương cùng chiều chuyển động
\(sin\alpha.P-\mu.N=m.a\) (2)
chiếu (1) lên trục Oy phương vuông gốc với mặt phẳng, chiều dương hướng lên trên
N=\(cos\alpha.P\) (3)
từ (2),(3)
\(\Rightarrow sin\alpha.g-\mu.g.cos\alpha=a\)
\(\Rightarrow a\approx4,1\)m/s2
vận tốc lúc vật tại B
\(v^2-v_0^2=2as_{AB}\Rightarrow v\approx2,875\)m/s
Đúng 0
Bình luận (1)
Một mặt phẳng AB nghiêng một góc 300 so với mặt phẳng ngang BC Biết AB =1m BC = 10,35 , hệ số ma sát trên mặt phẳng nghiêng là k1=0,1 lấy g =10m/s2. Một vật khối lượng m =1kg trượt không có vận tốc ban đầu từ đỉnh A tới C thì dừng lại. Tính vận tốc của vật tại B và hệ số ma sát k2 trên mặt phẳng ngang ?
Một vật có khối lượng m = 4kg trượt không vận tốc đầu từ điểm A có độ cao h=0,8m theo mp nghiêng AB không có ma sát.
a/ tính vận tốc của vật tại B.
b/ tới B vật tiếp tục trượt trên mặt phẳng nằm ngang BC tới C vật dừng lại. Tính BC hệ số ma sát trên BC là 0,25
a, Khi vật đang ở A, động năng của vật là cực đại và nó bằng thế năng của vật tại B (Wt max):
Wtmax = mgz = 4 . 10 . 0,8 = 32 (J)
⇒ \(\dfrac{1}{2}mv^2=32\)
⇒ v = 4 (m/s)
Vậy khi đến B v = 4 m/s
b, Do có lực ma sát nên cơ năng không được bảo toàn
Độ biến thiên cơ năng bằng công của lực ma sát
Tại B, cơ năng của vật là
W = Wđmax = 32 (J)
Tại C cơ năng của vật là
W = Wt + Wđ = 40. BC
Ta có 40BC - 32 = F . BC
⇒ 40BC - 32 = N . 0.25 . BC
⇒ 40BC - 32 = 10BC
⇒ BC = \(\dfrac{32}{30}=1,06\left(m\right)\)
Đúng 1
Bình luận (1)



















