cho 2 đoạn thẳng AB và CD bằng nhau và song song với nhau sao cho Ac < BD.Gọi O,E,F lần lượt là trung điểm của BO,AB,CD. chứng rỏ 3 điểm O,E,F thẳng hàng

Những câu hỏi liên quan
Cho 2 đoạn thẳng AB và CD song song với O là giao điểm của AC và BD.Lấy E trên AB,F trên CD sao cho \(\frac{EA}{EB}=\frac{FC}{FD}\).Chứng minh E,O,F thẳng hàng
Kéo dài \(EO\)cắt \(CD\)tại \(F'\).
Ta có: \(AE//CF'\Rightarrow\frac{AE}{CF'}=\frac{OE}{OF'}\)(theo Thalet)
\(EB//DF'\Rightarrow\frac{EB}{DF'}=\frac{OE}{OF'}\)(theo Thalet)
Suy ra \(\frac{EA}{F'C}=\frac{EB}{F'D}\Leftrightarrow\frac{EA}{EB}=\frac{F'C}{F'D}\Rightarrow F'\equiv F\).
Suy ra \(E,O,F\)thẳng hàng.
Trên cung nhỏ
A
B
⏜
của (O), cho hai điểm C và D sao cho cung
A
B
⏜
được chia thành ba cung bằng nhau (
A
C
⏜
C
D
⏜
D...
Đọc tiếp
Trên cung nhỏ A B ⏜ của (O), cho hai điểm C và D sao cho cung A B ⏜ được chia thành ba cung bằng nhau ( A C ⏜ = C D ⏜ = D B ⏜ ). Bán kính OC và OD cắt dây AB lần lượt tại E và F
a, Hãy so sánh các đoạn thẳng AE và FB
b, Chứng minh các đường thẳng AB và CD song song
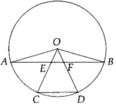
a, Chứng minh được ∆OEA = ∆OFB => AE = FB
b, Chứng minh được O E F ^ = O C D ^ => AB//CD
Đúng 0
Bình luận (0)
Cho hình thang ABCD ( AB//CD), Gọi M,N lần lượt là trung điểm của AB<CD, O là giao điểm của AC và BD; I là giao điểm của AD,BC
a) chứng minh O,I,M,N thẳng hàng
b) Qua O kẻ đường thẳng song song với AB cắt AD,BC lần lượt tại E,F. Chứng minh OE=OF
alodgdhgjkhukljhkljyutfruftyhf
Cho hình thang ABCD AB song song CD từ B và D lần lượt BM vuông góc AC và BD vuông góc AC chứng minh rằng tam giác ABM đồng dạng tam giác CDN minh rằng OA.OC=OB.OD Gọi E là trung điểm của AB ,F là trung điểm của CD Chứng minh O E F thẳng hàng
Cho hình thang ABCD có AB song song CD ( ABCD) và M là trung điểm của AD. Qua M vẽ đường thẳng song song với 2 đáy của hình thang cắt cạnh bên BC tại N và cắt 2 đường chéo BD và AC lần lượt tại E,F.a)Chứng minh rằng N,E,F lần lượt là trung điểm của BC,BD,AC.b)Gọi I là trung điểm của AB. Đường thẳng vuông góc với IE tại E và đường thẳng vuông góc với IF tại F cắt nhau ở K.Chứng minh KCKD
Đọc tiếp
Cho hình thang ABCD có AB song song CD ( AB<CD) và M là trung điểm của AD. Qua M vẽ đường thẳng song song với 2 đáy của hình thang cắt cạnh bên BC tại N và cắt 2 đường chéo BD và AC lần lượt tại E,F.
a)Chứng minh rằng N,E,F lần lượt là trung điểm của BC,BD,AC.
b)Gọi I là trung điểm của AB. Đường thẳng vuông góc với IE tại E và đường thẳng vuông góc với IF tại F cắt nhau ở K.Chứng minh KC=KD
cho hình thang ABCD có AB song song CD ( AB CD) và M là trung điểm của AD. Qua M vẽ đường thẳng song song với 2 đáy của hình thang cắt cạnh bên BC tại N và cắt 2 đường chéo BD và AC lần lượt tại E. F.a) Chứng mình rằng N, E, F lần lượt là trung điể cạnh BC , BD, AC.b) Gọi I là trung điểm của AB. Đuo82ng thẳng vuông góc với IE tại E và đường thẳng vuông góc với IF tại F cắt nhau ở K. Chứng minh KC KD.
Đọc tiếp
cho hình thang ABCD có AB song song CD ( AB< CD) và M là trung điểm của AD. Qua M vẽ đường thẳng song song với 2 đáy của hình thang cắt cạnh bên BC tại N và cắt 2 đường chéo BD và AC lần lượt tại E. F.
a) Chứng mình rằng N, E, F lần lượt là trung điể cạnh BC , BD, AC.
b) Gọi I là trung điểm của AB. Đuo82ng thẳng vuông góc với IE tại E và đường thẳng vuông góc với IF tại F cắt nhau ở K. Chứng minh KC = KD.
cho hình thang ABCD có AB song song CD ( AB CD) và M là trung điểm của AD. Qua M vẽ đường thẳng song song với 2 đáy của hình thang cắt cạnh bên BC tại N và cắt 2 đường chéo BD và AC lần lượt tại E. F.a) Chứng mình rằng N, E, F lần lượt là trung điể cạnh BC , BD, AC.b) Gọi I là trung điểm của AB. Đuo82ng thẳng vuông góc với IE tại E và đường thẳng vuông góc với IF tại F cắt nhau ở K. Chứng minh KC KD.
Đọc tiếp
cho hình thang ABCD có AB song song CD ( AB< CD) và M là trung điểm của AD. Qua M vẽ đường thẳng song song với 2 đáy của hình thang cắt cạnh bên BC tại N và cắt 2 đường chéo BD và AC lần lượt tại E. F.
a) Chứng mình rằng N, E, F lần lượt là trung điể cạnh BC , BD, AC.
b) Gọi I là trung điểm của AB. Đuo82ng thẳng vuông góc với IE tại E và đường thẳng vuông góc với IF tại F cắt nhau ở K. Chứng minh KC = KD.
a) Ta có:
+) M là trung điểm của AD và MN // CD
MN là đường trung bình của hình thang ABCD
N là trung điểm của BC
+) M là trung điểm của AB và ME // AB
ME là đường trung...
Đúng 1
Bình luận (0)
= một vé báo cáo chứ sao khó ợt
cho hình thang ABCD có AB song song CD ( AB CD) và M là trung điểm của AD. Qua M vẽ đường thẳng song song với 2 đáy của hình thang cắt cạnh bên BC tại N và cắt 2 đường chéo BD và AC lần lượt tại E. F.a) Chứng mình rằng N, E, F lần lượt là trung điể cạnh BC , BD, AC.b) Gọi I là trung điểm của AB. Đuo82ng thẳng vuông góc với IE tại E và đường thẳng vuông góc với IF tại F cắt nhau ở K. Chứng minh KC KD.
Đọc tiếp
cho hình thang ABCD có AB song song CD ( AB< CD) và M là trung điểm của AD. Qua M vẽ đường thẳng song song với 2 đáy của hình thang cắt cạnh bên BC tại N và cắt 2 đường chéo BD và AC lần lượt tại E. F.
a) Chứng mình rằng N, E, F lần lượt là trung điể cạnh BC , BD, AC.
b) Gọi I là trung điểm của AB. Đuo82ng thẳng vuông góc với IE tại E và đường thẳng vuông góc với IF tại F cắt nhau ở K. Chứng minh KC = KD.
Gọi H là trung điểm DC.
Chứng minh HE// IF( vì cùng //BC)
=> HE vuông FK ( vì FK vuông IF)
Tương tự HF// EI( vì cùng //AD)
=> HF vuông EK( vì EK vuông IE)
Xét tam giác EFH có EK và FK là 2 đường cao nên K là trực tâm. Suy ra HK vuông FE mà FE //DC nên HK vuông DC tại H suy ra tam giác KDC cân tại K. Nên KD=KC
Đúng 0
Bình luận (0)
cho hình thang ABCD(AB song song với CD).kẻ hai đường chéo AC và BD cắt nhau tại O cho tam giác ABO đều.các điểm E,F,G lần lượt là trung điểm của các đoạn thẳng OA,OD và BC .Chứng minh tam giác EFG đều

















