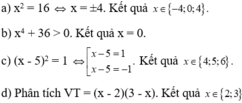tìm x biết √x4=3

Những câu hỏi liên quan
Tìm x, biết:
215+3:|x4−|−23||=6215+3:|x4−|−23||=6
?
bài 1:phân tích đa thức thành nhân tử
a,x4 +5x2 +9
b,x4 + 3x2 +4
c,2x4 - x2 -1
Bài 2:tìm x biết
a,(x+1) (x+2)(x+3)(x+4)= 120
b,(x-4x+3)(x2+6x +8) +24
Bài 1:
\(a,x^4+5x^2+9\\=(x^4+6x^2+9)-x^2\\=[(x^2)^2+2\cdot x^2\cdot3+3^2]-x^2\\=(x^2+3)^2-x^2\\=(x^2+3-x)(x^2+3+x)\)
\(b,x^4+3x^2+4\\=(x^4+4x^2+4)-x^2\\=[(x^2)^2+2\cdot x^2\cdot2+2^2]-x^2\\=(x^2+2)^2-x^2\\=(x^2+2-x)(x^2+2+x)\)
\(c,2x^4-x^2-1\\=2x^4-2x^2+x^2-1\\=2x^2(x^2-1)+(x^2-1)\\=(x^2-1)(2x^2+1)\\=(x-1)(x+1)(2x^2+1)\)
Đúng 1
Bình luận (2)
Bài 2:
\(a,\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)=120\)
\(\Leftrightarrow\left[\left(x+1\right)\left(x+4\right)\right]\cdot\left[\left(x+2\right)\left(x+3\right)\right]=120\)
\(\Leftrightarrow\left(x^2+5x+4\right)\left(x^2+5x+6\right)=120\) (1)
Đặt \(x^2+5x+5=y\), khi đó (1) trở thành:
\(\left(y-1\right)\left(y+1\right)=120\)
\(\Leftrightarrow y^2-1=120\)
\(\Leftrightarrow y^2=121\)
\(\Leftrightarrow\left[{}\begin{matrix}y=11\\y=-11\end{matrix}\right.\)
+, TH1: \(y=11\Leftrightarrow x^2+5x+5=11\)
\(\Leftrightarrow x^2+5x-6=0\)
\(\Leftrightarrow x^2-x+6x-6=0\)
\(\Leftrightarrow x\left(x-1\right)+6\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x+6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-6\end{matrix}\right.\left(\text{nhận}\right)\)
+, TH2: \(y=-11\Leftrightarrow x^2+5x+5=-11\)
\(\Leftrightarrow x^2+5x+16=0\)
\(\Leftrightarrow\left[x^2+2\cdot x\cdot\dfrac{5}{2}+\left(\dfrac{5}{2}\right)^2\right]-\dfrac{25}{4}+16=0\)
\(\Leftrightarrow\left(x+\dfrac{5}{2}\right)^2+\dfrac{39}{4}=0\)
Ta thấy: \(\left(x+\dfrac{5}{2}\right)^2\ge0\forall x\)
\(\Rightarrow\left(x+\dfrac{5}{2}\right)^2+\dfrac{39}{4}\ge\dfrac{39}{4}>0\forall x\)
Mà \(\left(x+\dfrac{5}{2}\right)^2+\dfrac{39}{4}=0\)
\(\Rightarrow\) loại
Vậy \(x\in\left\{1;-6\right\}\).
\(b,\) Đề thiếu vế phải rồi bạn.
Đúng 1
Bình luận (0)
Tìm đa thức M biết:a)
2
x
6
-
x
4
-
2
x
2
+1 M.(2
x
2
-1);b) (
x
2
+x + 1).M
x
4
-
x
3
- 4
x
2
- 5x - 3.
Đọc tiếp
Tìm đa thức M biết:
a) 2 x 6 - x 4 - 2 x 2 +1 = M.(2 x 2 -1);
b) ( x 2 +x + 1).M = x 4 - x 3 - 4 x 2 - 5x - 3.
a) Kết quả M = x 4 – 1.
b) Kết quả M = x 2 – 2x – 3.
Đúng 0
Bình luận (0)
Tìm x,y thuộc Z biết x4+2x3+2x2+x+3=y2
giúp mình với ạ
Bài 3: cho đa thức P(x)= 5x3 - x4 + 2x - x2 + x4 + 2x2 - 5x3 - 3
a, thu gọn tìm bậc của đa thức
b, Chứng tỏ X=-3 ; x=1 là các nghiệm của đa thức P(x)
c, Tìm nghiệm của đa thức Q(x) biết Q(x) + P(x) = x2 - x
Cần gấp
a. cậu thu gọn bằng cách dùng t/c kết hợp và giao hoán
b. cậu thay từng giá vào biểu thức vừa được rút gọn để tìm
c. thì.... tớ ko biết
Đúng 1
Bình luận (0)
Tìm x biết rằng:a) (
x
2
+ 2x + 4)(2 - x) + x(x - 3)(x + 4) -
x
2
+ 24 0;b)
x
2
+
3
(
5
−
6
x
)
+
(
12
x
−
2
)
x
4
+...
Đọc tiếp
Tìm x biết rằng:
a) ( x 2 + 2x + 4)(2 - x) + x(x - 3)(x + 4) - x 2 + 24 = 0;
b) x 2 + 3 ( 5 − 6 x ) + ( 12 x − 2 ) x 4 + 3 = 0 .
Cho các đa thức:
f(x) = x4 – 3x2 + x – 1
g(x) = x4 – x3 + x2 + 5
Tìm h(x) biết f(x) + h(x) = g(x)
Ta có: f(x) + h(x) = g(x)
Suy ra: h(x) = g(x) – f(x) = (x4 – x3 + x2 + 5) – (x4 – 3x2 + x – 1)
= x4 – x3 + x2 + 5 – x4 + 3x2 – x + 1
= ( x4 – x4) – x3 + (x2 + 3x2 ) – x + (5+ 1)
= -x3 + 4x2 – x + 6
Đúng 0
Bình luận (0)
Cho các đa thức:
f(x) = x4 – 3x2 + x – 1
g(x) = x4 – x3 + x2 + 5
Tìm h(x) biết f(x) – h(x) = g(x)
Ta có: f(x) – h(x) = g(x)
Suy ra: h(x) = f(x) – g(x) = (x4 – 3x2 + x – 1) – (x4 – x3 + x2 + 5)
= x4 – 3x2 + x – 1 – x4 + x3 – x2 – 5
= (x4 – x4) + x3 – (3x2 + x2) + x - (1+ 5)
= x3 – 4x2 + x – 6
Đúng 0
Bình luận (0)
Tìm x, biết:a)
(
x
+
3
)
2
+ (4 - x)(x + 4) 1;b)
(2 - x)
3
+(3 +x)(9 - 3x +
x
2
) + 6x(1 - x) 17;c)
x
4
- 2
x
2
+1 0.
Đọc tiếp
Tìm x, biết:
a) ( x + 3 ) 2 + (4 - x)(x + 4) = 1;
b) (2 - x) 3 +(3 +x)(9 - 3x + x 2 ) + 6x(1 - x) = 17;
c) x 4 - 2 x 2 +1 = 0.
a) Tìm được x = -4.
b) Tìm được x = 3.
c) Tìm được x = ±1.
Đúng 0
Bình luận (0)
Tìm x, biết: a)
x
4
-
16
x
2
0; c)
x
8
+
36
x
4
0; b)
(
x
-
5
)
3
- x + 5...
Đọc tiếp
Tìm x, biết:
a) x 4 - 16 x 2 =0; c) x 8 + 36 x 4 =0;
b) ( x - 5 ) 3 - x + 5 = 0; d) 5(x - 2 ) - x 2 + 4 = 0.