cho a thuộc N; chứng tỏ rằng : UCLN (2n-5;3n+8)

Những câu hỏi liên quan
Cho a^m=a^n (a thuộc Q; m,n thuộc N) tìm các số m và n
cho a^m>a^n (a thuộc Q ; a>0;m,n thuộc N) so sánh m và n
Cho a^m=a^n ( a thuộc Q; m,n thuộc N); b) Cho a^m> a^n (a thuộc Q; a>0; m,n thuộc N). Mình cần gấp,ai giúp mik với
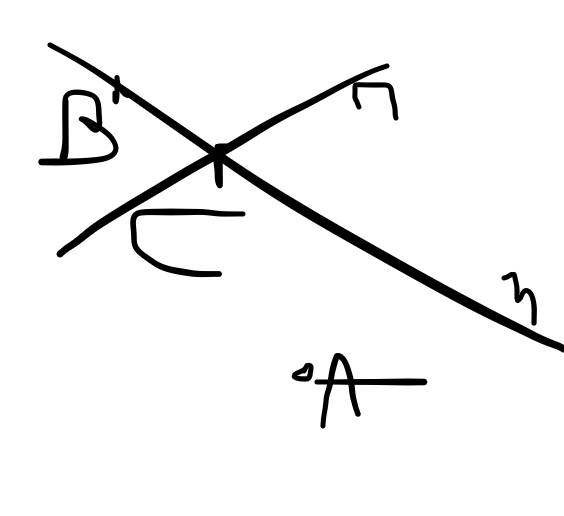
Cho hai đường thẳng m, n
a) Vẽ điểm A sao cho A không thuộc m và không thuộc n
b) Vẽ điểm B sao cho B thuộc m và B không thuộc n
c) Vẽ điểm C sao cho C thuộc m và C thuộc n
cho A= 3/ n-2 ; n thuộc Z. Tìm n để A thuộc Z
Cho b= n/n+1 ; n thuộc Z. Tìm n để B thuộc Z
A nguyên <=> 3 ⋮ n - 2
=> n - 2 thuộc Ư(3)
=> n - 2 thuộc {-1;1;-3;3}
=> n thuộc {1;3;-1;5}
B nguyên <=> n ⋮ n + 1
=> n + 1 - 1 ⋮ n + 1
=> 1 ⋮ n + 1
=> như a
ĐK : \(n\ne2\)
\(A=\frac{3}{n-2}\Rightarrow n-2\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)
| n - 2 | 1 | -1 | 3 | -3 |
| n | 3 | 1 | 5 | -1 |
ĐK : \(n\ne-1\)
\(B=\frac{n}{n+1}=\frac{n+1-1}{n+1}=1-\frac{1}{n+1}\)
\(\Rightarrow n+1\inƯ\left(1\right)=\left\{\pm1\right\}\)
| n + 1 | 1 | -1 |
| n | 0 | -2 |
Cho 2 đường thẳng m,n
a) Về điểm A sao cho A không thuộc m và A không thuộc n
b) Vẽ điểm B sao cho B thuộc m và B không thuộc n
c) Về điểm C sao cho c thuộc m và C thuộc n
1. cho n thuộc z
c/m a=n^4-n^2 chia hết cho 12
2.cho n thuộc z
c/m a= n^2(n^4-1) chia hết cho 60
3.cho n thuộc z
c/m a=2n(16-n^4) chia hết cho 30
4.cho a,b thuộc z
c/m M=ab(a^4-b^4) chia hết cho 30
Cho hai đường thẳng m, n
a) Vẽ điểm A sao cho A không thuộc m và không thuộc n
b) Vẽ điểm B sao cho B thuộc m và B không thuộc n
c) Vẽ điểm C sao cho C thuộc m và C thuộc n
Tìm các số m và n thỏa mãn:a^m và a^n(a thuộc Q và m,n thuộc N)
Cho a^m>a^n(a thuộc ,a>0 và m,n thuộc N)so sanh m và n
Câu a
Nếu a=0 thì m và n là các số tự nhiên khác 0 tùy ý
a=1 thì m và n là các số tự nhiên tùy ý
a=-1 thì m và n là các số chẵn tùy ý hoặc các số lẻ tùy ý
a khác 0,a khác+_ 1 thì m=n
Câu b
Nếu a>1 thì m>n
Nếu 0<a<1 thì m<n
Đúng 0
Bình luận (0)
Cho A=n+1/n-2 (n thuộc Z)
tìm n thuộc Z để A thuộc Z
Để A € Z
Thì n+1 chia hết cho n—2
==> n—2+3 chia hết cho n—2
Vì n—2 chia hết cho n—2
Nên 3 chia hết cho n—2
==> n—2 € Ư(3)
==> n—2 € {1;—1;3;—3}
Ta có
TH1: n—2=1
n=1+2
n=3
TH2: n—2=—1
n=—1+2
n=1
TH3: n—2=3
n=3+2
n=5
TH4: n—2=—3
n=—3+2
n=—1
Vậy n € {3;1;5;—1}
Đúng 0
Bình luận (0)
cho mink hỏi cho a thuộc Z b thuộc Z (b khác 0) n thuộc N* hãy so sánh a/bvaf a+n/ b+n
+) Xét trường hợp \(\dfrac{a}{b}>1\Rightarrow\) \(a>b\Rightarrow an>bn\) (do \(n\in\) N*)\(\Rightarrow an+ab>bn+ab\Rightarrow a.\left(b+n\right)>b.\left(a+n\right)\Rightarrow\dfrac{a}{b}>\dfrac{a+n}{b+n}\)
+) Xét trường hợp \(\dfrac{a}{b}\le1\Rightarrow\)\(a\le b\Rightarrow an\le bn\) (do \(n\in\) N*)
\(\Rightarrow an+ab\le bn+ab\Rightarrow a.\left(b+n\right)\le b.\left(a+n\right)\Rightarrow\dfrac{a}{b}\le\dfrac{a+n}{b+n}\)
Vậy nếu \(\dfrac{a}{b}>1\) thì \(\dfrac{a}{b}>\dfrac{a+n}{b+n}\); nếu \(\dfrac{a}{b}\le1\) thì \(\dfrac{a}{b}\le\dfrac{a+n}{b+n}\).
Đúng 0
Bình luận (5)