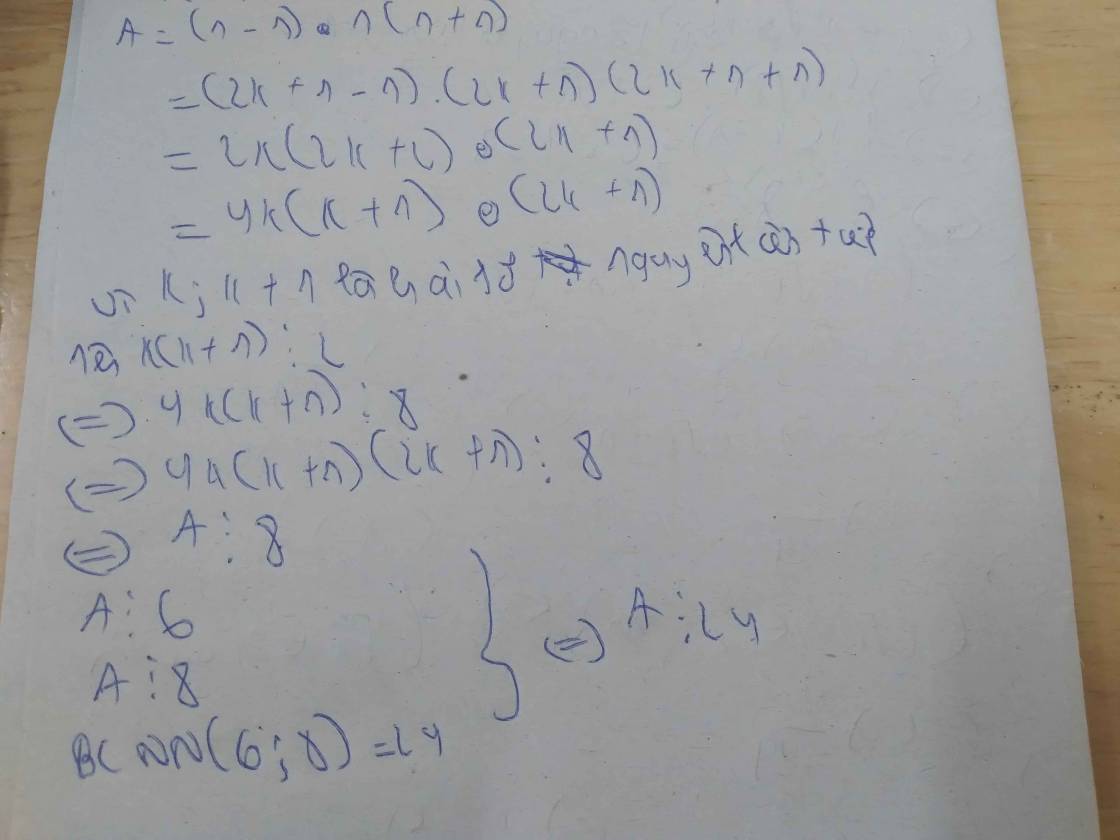cmr :với a;b;c là số dương thì \(\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge9\)

Những câu hỏi liên quan
a, Với n lẻ cmr A= (n-1) n (n+1) ⋮ 24
b,Với n lẻ cmr n2 - 1 ⋮ 8
Cho hình chóp S.ABCD đáy là hình vuông, SA vuông góc với (ABCD) a) CMR : BC vuông góc với (SAB); CD vuông góc với (SAD) b) CMR : BD vuông góc với (SAC) c) Kẻ AE vuông góc với SB. CMR : SB vuông góc với (ADE)
Cho ∆ABC cân tại A. Kẻ AH vuông BC CH B a CMR ∆BABH ∆ACH b CMR BAH CAH c Qua C kẻ đường thẳng song song với AB cắt AC tại E. CMR ∆HEC cân tại E CmR E là trung điểm AC Giúp mih nhanh lên với huhuhu
Xem chi tiết
dễ mak :)))))))))))))))))))))))))))))))))))))))))))))))))))))))
cho ΔABC vuông tại A . Đường cao AH, kẻ HE vuông góc với AB (E thuộc AB), kẻ HF vuông góc với AC (F thuộc AC)
a . CMR: AEHF là hình chữ nhật
b . CMR: ΔAEF đồng dạng với ΔACB
c . Vẽ trung truyến AM CMR: AM vuông góc EF
a: Xét tứ giác AEHF có
góc AEH=góc AFH=góc FAE=90 độ
=>AEHF là hình chữ nhật
b: ΔHAB vuông tại H có HE là đường cao
nên AE*AB=AH^2
ΔAHC vuông tại H có HF là đường cao
nên AF*AC=AH^2
=>AE*AB=AF*AC
=>AE/AC=AF/AB
Xét ΔAEF và ΔACB có
AE/AC=AF/AB
góc A chung
=>ΔAEF đồng dạng với ΔACB
c: góc AFE+góc MAC
=góc C+góc AHE
=góc C+góc ABC=90 độ
=>AM vuông góc EF
Đúng 0
Bình luận (0)
cho tam giác abc có góc a bằng góc b.tia pg góc a cắt bc tại d .
a)cmr tam giác adb=adc
b)cmr ab=ac
c)cmr ad vuông góc với bc
a: Xét ΔADB và ΔADC có
\(\widehat{BAD}=\widehat{CAD}\)
AD chung
\(\widehat{B}=\widehat{C}\)
Do đó: ΔADB=ΔADC
Đúng 0
Bình luận (0)
4. chứng minh rằng
a) CMR tổng 5 số tự nhiên chia hết cho 5
b)CMR n2+n chia hết cho 2 với n thuộc N
c) CMR a2b + b2a chia hết cho 2 với a,b thuộc N
d) CMR 51n + 47102 chia hết cho 10 (n thuộc N)
CMR: chứng minh rằng
a) Gọi 5 số tự nhiên đó là a; a+1; a+2; a+3;a+4
Tổng 5 số đó là a + a+1 + a+2 + a+3 + a+4
= (a+a+a+a+a) + (1+2+3+4)
= 5a + 10
= 5(a+2) chia hết cho 5
Vậy tổng của 5 số tự nhiên chia hết cho 5
Đúng 0
Bình luận (0)
cho △ABC vuông tại A, phân giác AD. Đường thẳng qua D vuông góc với BC, cắt AB, AC lần lượt tại I,E
a) CMR AB.CD= AC.DB và CI vuông góc với BE
b) CMR △ABC đồng dạng với △DEC và AC.BE = AD.BC
c) CMR DB= DE
d0 cho AC = 28cm; BC = 35cm. Tính AB, DC và S△DBE
a: Xet ΔABC có AD là phân giác
nên AB/AC=DB/DC
=>AB*DC=DB*AC
Xét ΔCIB có
CA,ID là đường cao
CA cắt ID tại E
=>E là trựctâm
=>BE vuông góc CI
b: Xét ΔCDE vuông tại D và ΔCAB vuông tại A có
góc C chung
=>ΔCDE đồng dạng với ΔCAB
c: ΔCDE đồng dạng với ΔCAB
=>DE/AB=CD/CA=BD/BA
=>DE=DB
Đúng 0
Bình luận (0)
CMR tổng 5 số tự nhiên liên tiếp chia hết cho 5
CMR n2+n chia hết cho 2 với nn thuộc N
CMR a2b + b2a chia hết cho 2 với a,b thuộc N
CMR 51n+47102chia hết cho 10 (n thuộc N)
a, CMR a^3 + 5.a chia hết cho 6 ( với mọi a thuộc N )
b, Cho a+b+c =60 . CMR a^3 + b^3 + c^3 chia hết cho 6 với mọi a,b,c thuộc N
Cho xoy = 90 độ; M nằm trong xoy' kẻ đường thẳng a vuông góc với Ox và đường thẳng b vuông góc với Oy
a/ CMR: a//Oy
b/ CMR: bB//Ox
Bạn tự vẽ hình nha![]()
a.
a _I_ OxOy _I_ Ox=> a // Oy
b.
b _I_ OyOx _I_ Oy=> b // Ox
Chúc bạn học tốt![]()
Đúng 0
Bình luận (0)