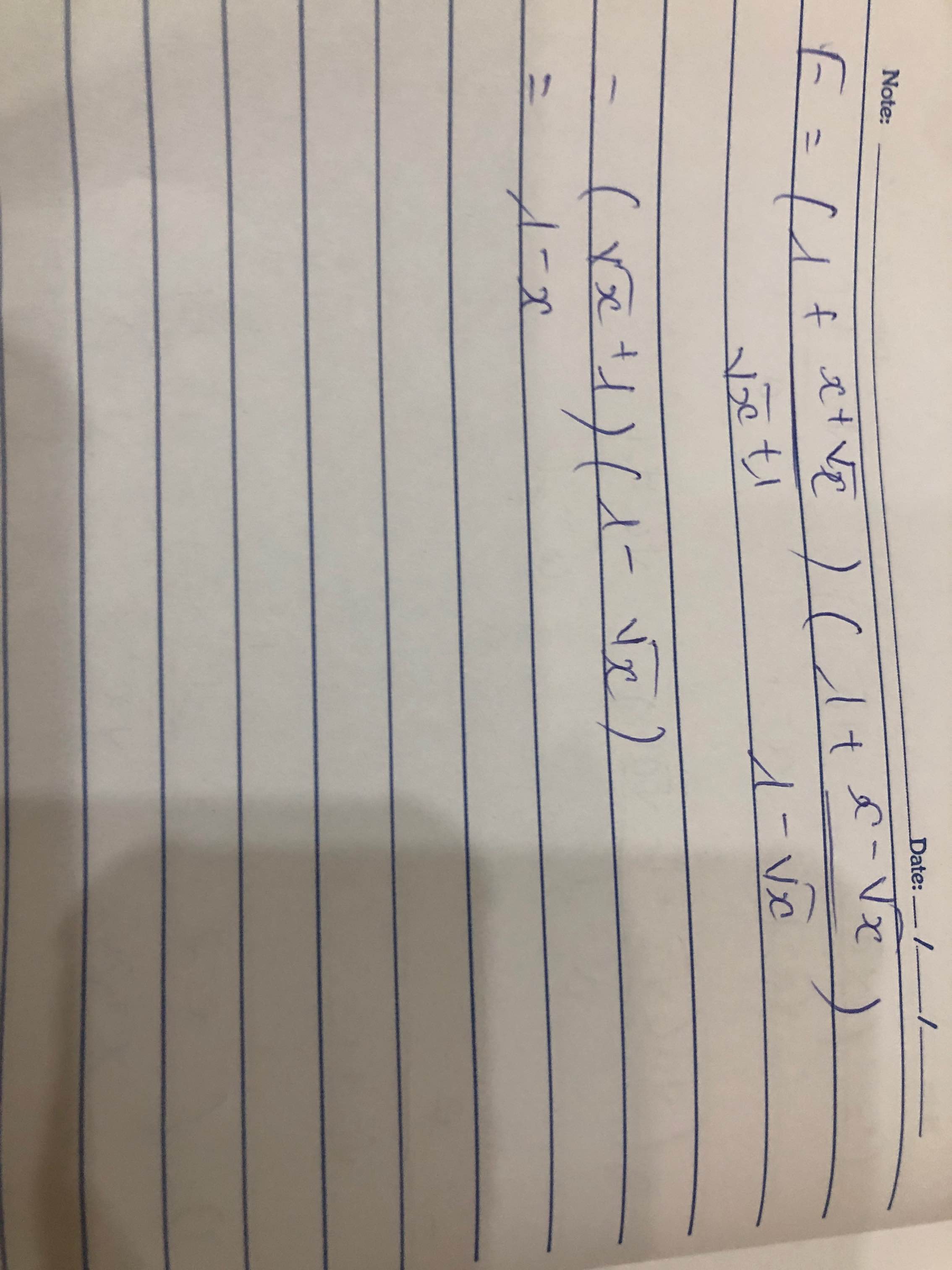ĐKXĐ: \(\left\{{}\begin{matrix}a>=0\\a< >1\end{matrix}\right.\)

\(\left(\dfrac{a+3\sqrt{a}+2}{\left(\sqrt{a}+2\right)\left(\sqrt{a}-1\right)}-\dfrac{a\sqrt{a}}{a-1}\right)\cdot\left(\dfrac{1}{\sqrt{a}+1}+\dfrac{1}{\sqrt{a}-1}\right)\)

\(=\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-1}-\dfrac{a\sqrt{a}}{a-1}\right)\cdot\dfrac{\sqrt{a}-1+\sqrt{a}+1}{a-1}\)

\(=\dfrac{\left(\sqrt{a}+1\right)^2-a\sqrt{a}}{a-1}\cdot\dfrac{2\sqrt{a}}{a-1}\)

\(=\dfrac{2\sqrt{a}\left(a+2\sqrt{a}+1-a\sqrt{a}\right)}{\left(a-1\right)^2}\)

A = \(\left(\dfrac{a-1}{\sqrt{a}-1}-2\right)\left(\dfrac{a-\sqrt{a}}{\sqrt{a}-1}+1\right)=\left(\dfrac{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}{\sqrt{a}-1}-2\right)\left(\dfrac{\sqrt{a}\left(\sqrt{a}-1\right)}{\sqrt{a}-1}+1\right)=\left(\sqrt{a}+1-2\right)\left(\sqrt{a}+1\right)=\left(\sqrt{a}-1\right)\left(\sqrt{a}-1\right)=a-1\)

\(B=\left(\dfrac{a\sqrt{a}-a}{a-\sqrt{a}}-\dfrac{a\sqrt{a}+1}{a+\sqrt{a}}\right):\dfrac{a+2}{a-2}=\left(\dfrac{a\left(\sqrt{a}-1\right)}{\sqrt{a}\left(\sqrt{a}-1\right)}-\dfrac{\left(\sqrt{a}+1\right)\left(a-\sqrt{a}+1\right)}{\sqrt{a}\left(\sqrt{a}+1\right)}\right)\cdot\dfrac{a-2}{a+2}=\left(\dfrac{a}{\sqrt{a}}-\dfrac{a-\sqrt{a}+1}{\sqrt{a}}\right)\cdot\dfrac{a-2}{a+2}=\dfrac{\sqrt{a}-1}{\sqrt{a}}\cdot\dfrac{a-2}{a+2}=\dfrac{\left(\sqrt{a}-1\right)\left(a-2\right)}{\sqrt{a}\left(a+2\right)}\)

\(C=\left(\dfrac{\sqrt{a}}{\sqrt{a}-1}-\dfrac{a}{a-1}\right):\left(\sqrt{a}-\dfrac{\sqrt{a}}{\sqrt{a}+1}\right)=\left(\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)}{a-1}-\dfrac{a}{a-1}\right):\left(\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)-\sqrt{a}}{\sqrt{a}+1}\right)=\dfrac{\sqrt{a}}{a-1}:\dfrac{a}{\sqrt{a}+1}=\dfrac{\sqrt{a}}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\cdot\dfrac{\sqrt{a}+1}{a}=\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}\)

\(D=\dfrac{a+\sqrt{a}}{\sqrt{a}}+\dfrac{a+4}{\sqrt{a}+2}=\sqrt{a}+1+\dfrac{a+4}{\sqrt{a}+2}=\dfrac{\sqrt{a}\left(\sqrt{a}+2\right)+\sqrt{a}+2+a+4}{\sqrt{a}+2}=\dfrac{a+2\sqrt{a}+\sqrt{a}+2+a+4}{\sqrt{a}+2}=\dfrac{2a+3\sqrt{a}+6}{\sqrt{a}+2}\)

\(E=\left(\sqrt{a}-\dfrac{1}{\sqrt{a}}\right)\left(\dfrac{\sqrt{a}-1}{\sqrt{a}}+\dfrac{1-\sqrt{a}}{a+\sqrt{a}}\right)=\dfrac{a-1}{\sqrt{a}}\cdot\dfrac{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)+1-\sqrt{a}}{\sqrt{a}\left(\sqrt{a}+1\right)}=\dfrac{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}{\sqrt{a}}\cdot\dfrac{a-1+1-\sqrt{a}}{\sqrt{a}\left(\sqrt{a}+1\right)}=\dfrac{\left(\sqrt{a}-1\right)\cdot\sqrt{a}\left(\sqrt{a}-1\right)}{\sqrt{a}\cdot\sqrt{a}}=\dfrac{\left(\sqrt{a}-1\right)^2}{\sqrt{a}}\)

\(P=\left(\dfrac{\sqrt{a}}{2}-\dfrac{1}{2\sqrt{a}}\right)^2.\left(\dfrac{\sqrt{a}-1}{\sqrt{a}+1}-\dfrac{\sqrt{a}+1}{\sqrt{a}-1}\right)\)

   \(=\left(\dfrac{a-1}{2\sqrt{a}}\right)^2.\left(\dfrac{\left(\sqrt{a}-1\right)^2-\left(\sqrt{a}+1\right)^2}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\right)\)

   \(=\dfrac{\left(a-1\right)^2}{4a}.\dfrac{-4\sqrt{a}}{a-1}=\dfrac{1-a}{\sqrt{a}}\)

Ta có: \(P=\left(\dfrac{\sqrt{a}}{2}-\dfrac{1}{2\sqrt{a}}\right)^2\cdot\left(\dfrac{\sqrt{a}-1}{\sqrt{a}+1}-\dfrac{\sqrt{a}+1}{\sqrt{a}-1}\right)\)

\(=\dfrac{\left(\sqrt{a}-1\right)^2\cdot\left(\sqrt{a}+1\right)^2}{4a}\cdot\dfrac{a-2\sqrt{a}+1-a-2\sqrt{a}-1}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\)

\(=\dfrac{a-1}{4a}\cdot\dfrac{-4\sqrt{a}}{1}\)

\(=\dfrac{-a+1}{\sqrt{a}}\)

Ta có: \(\left(\dfrac{\sqrt{a}}{2}-\dfrac{1}{2\sqrt{a}}\right)\left(\dfrac{a\sqrt{a}}{\sqrt{a}+1}-\dfrac{a+\sqrt{a}}{\sqrt{a}-1}\right)\)

\(=\dfrac{a-1}{2\sqrt{a}}\cdot\dfrac{a\sqrt{a}\left(\sqrt{a}-1\right)-\sqrt{a}\left(\sqrt{a}+1\right)^2}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\)

\(=\dfrac{\sqrt{a}\left[a\left(\sqrt{a}-1\right)-\left(\sqrt{a}+1\right)^2\right]}{2\sqrt{a}}\)

\(=\dfrac{a\sqrt{a}-a-a-2\sqrt{a}-1}{2}\)

\(=\dfrac{-2a+a\sqrt{a}-2\sqrt{a}-1}{2}\)

\(\left(\dfrac{\sqrt{a}}{2}-\dfrac{1}{2\sqrt{a}}\right)\left(\dfrac{a\sqrt{a}}{\sqrt{a}+1}-\dfrac{a+\sqrt{a}}{\sqrt{a}-1}\right)\)

\(=\left(\dfrac{a-1}{2\sqrt{a}}\right)\left(\dfrac{a^2-a\sqrt{a}-a\sqrt{a}-a-a-\sqrt{a}}{a-1}\right)\)

\(=\dfrac{a^2-3a\sqrt{a}-2a}{2\sqrt{a}}\)

\(\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-1}-\dfrac{\sqrt{a}-1}{\sqrt{a}+1}+4\sqrt{a}\right)\left(\sqrt{a}-\dfrac{1}{\sqrt{a}}\right)\)

Với `x >= 0,x ne 4` có:

`M=[(\sqrt{x}+1)(\sqrt{x}+2)+2\sqrt{x}(\sqrt{x}-2)-2-5\sqrt{x}]/[(\sqrt{x}-2)(\sqrt{x}+2)]`

`M=[x+3\sqrt{x}+2+2x-4\sqrt{x}-2-5\sqrt{x}]/[(\sqrt{x}-2)(\sqrt{x}+2)]`

`M=[3x-6\sqrt{x}]/[(\sqrt{x}-2)(\sqrt{x}+2)]=[3\sqrt{x}]/[\sqrt{x}+2]`

____________

`N=(1/[\sqrt{a}-1]-1/\sqrt{a}):([\sqrt{a}+1]/[\sqrt{a}-2]-[\sqrt{a}+2]/[\sqrt{a}-1])`

      - Biểu thức `N` là như vầy?

Với `a > 0,a ne 1,a ne 4` có:

`N=[\sqrt{a}-\sqrt{a}+1]/[\sqrt{a}(\sqrt{a}-1)]:[(\sqrt{a}+1)(\sqrt{a}-1)-(\sqrt{a}+2)(\sqrt{a}-2)]/[(\sqrt{a}-2)(\sqrt{a}-1)]`

`N=1/[\sqrt{a}(\sqrt{a}-1)].[(\sqrt{a}-2)(\sqrt{a}-1)]/[a-1-a+4]`

`N=[\sqrt{a}-2]/[3\sqrt{a}]`

Với \(x\ge0;x\ne4\)

Khi đó:

\(M=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)}{x-4}+\dfrac{2\sqrt{x}\left(\sqrt{x}-2\right)}{x-4}-\dfrac{2+5\sqrt{x}}{x-4}\\ =\dfrac{x+2\sqrt{x}+\sqrt{x}+2}{x-4}+\dfrac{2x-4\sqrt{x}}{x-4}-\dfrac{2+5\sqrt{x}}{x-4}\\ =\dfrac{x+3\sqrt{x}+2+2x-4\sqrt{x}-2-5\sqrt{x}}{x-4}\\ =\dfrac{3x-6\sqrt{x}}{x-4}\\ =\dfrac{3\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\\ =\dfrac{3\sqrt{x}}{\sqrt{x}+2}\)

Với \(a>0;a\ne1;a\ne4\) 

Khi đó:

\(N=(\dfrac{\sqrt{a}}{\sqrt{a}\left(\sqrt{a}-1\right)}-\dfrac{\sqrt{a}-1}{\sqrt{a}\left(\sqrt{a}-1\right)}):\left(\dfrac{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}-\dfrac{\left(\sqrt{a}+2\right)\left(\sqrt{a}-2\right)}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}\right)\\ =\left(\dfrac{\sqrt{a}}{a-\sqrt{a}}-\dfrac{\sqrt{a}-1}{a-\sqrt{a}}\right):\left(\dfrac{a-1}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}-\dfrac{a-4}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}\right)\\ =\dfrac{1}{a-\sqrt{a}}:\dfrac{a-1-a+4}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}\\ =\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}.\dfrac{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}{3}\\ =\dfrac{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}{\sqrt{a}\left(\sqrt{a}-1\right).3}\\ =\dfrac{\sqrt{a}-2}{3\sqrt{a}}\)

Làm ơn giúp mình với... :(

bạn chụp rõ hơn dc không ạ? :( 

ĐKXĐ: \(\left\{{}\begin{matrix}a>0\\a\notin\left\{1;4\right\}\end{matrix}\right.\)

\(Q=\left(\dfrac{1}{\sqrt{a}-1}-\dfrac{1}{\sqrt{a}}\right):\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-2}-\dfrac{\sqrt{a}+2}{\sqrt{a}-1}\right)\)

\(=\dfrac{\sqrt{a}-\left(\sqrt{a}-1\right)}{\sqrt{a}\left(\sqrt{a}-1\right)}:\dfrac{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)-\left(\sqrt{a}-2\right)\left(\sqrt{a}+2\right)}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}\)

\(=\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}{a-1-a+4}\)

\(=\dfrac{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}{3\sqrt{a}\left(\sqrt{a}-1\right)}=\dfrac{\sqrt{a}-2}{3\sqrt{a}}\)

A=\(\left[\dfrac{\left(\sqrt{a}+2\right)\left(\sqrt{a}+1\right)}{\left(a-1\right)\left(\sqrt{a}+2\right)}-\dfrac{\left(a+\sqrt{a}\right)}{\left(a-1\right)}\right]\)::::::::\(\left(\dfrac{\left(\sqrt{a}-1+\sqrt{a}+1\right)}{a-1}\right)\)

=\(\left[\dfrac{1}{\sqrt{a}-1}\right]:\left(\dfrac{2\sqrt{a}}{a-1}\right)\)=\(\dfrac{\sqrt{a}-1}{2\sqrt{a}}\)

=\(\dfrac{a^2+a\sqrt{a}+11a+6}{2\sqrt{a}\left(\sqrt{a}+2\right)}\)

Ta có: \(A=\left(\dfrac{a+3\sqrt{a}+2}{\left(\sqrt{a}+2\right)\left(\sqrt{a}-1\right)}-\dfrac{a+\sqrt{a}}{a-1}\right):\left(\dfrac{1}{\sqrt{a}+1}+\dfrac{1}{\sqrt{a}-1}\right)\)

\(=\dfrac{\sqrt{a}+1-\sqrt{a}}{\sqrt{a}-1}:\dfrac{\sqrt{a}-1+\sqrt{a}+1}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\)

\(=\dfrac{1}{\sqrt{a}-1}\cdot\dfrac{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}{2\sqrt{a}}\)

\(=\dfrac{\sqrt{a}+1}{2\sqrt{a}}\)

ai giúp với ạ :<

2: Ta có: \(A=\left(\dfrac{1}{\sqrt{a}-1}-\dfrac{1}{\sqrt{a}}\right):\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-2}-\dfrac{\sqrt{a}+2}{\sqrt{a}-1}\right)\)

\(=\dfrac{\sqrt{a}-\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}-1\right)}:\dfrac{a-1-a+4}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}\)

\(=\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}{3}\)

\(=\dfrac{\sqrt{a}-2}{3\sqrt{a}}\)

1: Ta có: \(A=\left(\dfrac{x-5\sqrt{x}}{x-25}-1\right):\left(\dfrac{25-x}{x+2\sqrt{x}-15}-\dfrac{\sqrt{x}+3}{\sqrt{x}+5}-\dfrac{\sqrt{x}-5}{\sqrt{x}-3}\right)\)

\(=\left(\dfrac{x-5\sqrt{x}-x+25}{\left(\sqrt{x}-5\right)\left(\sqrt{x}+5\right)}\right):\dfrac{25-x-x+9-x+25}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-3\right)}\)

\(=\dfrac{-5}{\sqrt{x}+5}\cdot\dfrac{\left(\sqrt{x}+5\right)\left(\sqrt{x}-3\right)}{-3x+59}\)

\(=\dfrac{-5\left(\sqrt{x}-3\right)}{-3x+59}\)

\(=\dfrac{5\sqrt{x}-15}{3x-59}\)