Cho tâm giác ABC biết A-B = B-C = 10 độ. Tính các góc của tam giác ABC
Giúp mình với 😭😭 cần gấp
Cho ΔΔABC có góc BAC = 75 độ, góc ABC= 35 độ. Phân giác của góc BAC cắt cạnh BC tại D. Đường thẳng qa A và vuông góc với AD cắt tia BC tại E. Gọi M là trung điểm của DE. Chứng minh rằng:
a) Tam giác ACM cân
c) Chu vi tam giác ABC bằng độ dài đoạn thằng BE
Mình cần gấp😭😭😭😭😭
Xét tam giác ABC ta có
\(\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180\sigma\)
=> \(\widehat{ACB}=70\sigma\)
=> \(\widehat{BAD}=\widehat{CAD}\)= 37,5 độ
+ \(\widehat{BAE}\)= 37,5 độ + 90 độ = 127,5 độ
=> góc AEB = 180 độ - ( 35 độ + 127,5 độ )
=> góc AEB = 17,5 độ
+tam giác DAE vuông tại A có đường trung tuyến AM
=> AM = 1/2 DE => AM = ME = MD
+ AM = ME => tam giác AME cân tại M
=> góc AEM = góc EAM = 17,5 độ
+ góc AMC = góc AEM + góc EAM ( tính chất góc ngoài )
=> góc AMC = 17,5 độ + 17,5 độ = 35 độ
+ \(\widehat{ACB}=\widehat{AMC}+\widehat{CAM}\)=> góc CAM = góc ACB - góc AMC = 35 độ
=> \(\widehat{AMC}=\widehat{CAM}\)
=> tam giác ACM cân tại C ( đpcm )
c) Tam giác ACM cân tại C => AC = CM
góc ABC = góc AMC => tam giác ABM cân tại A
=> AB = AM => AB = ME ( AM = ME )
+ Chu vi tam giác ABC = AB + AC + BC
= ME + MC + BC = BE
=> chu vi tam giác ABC bằng độ dài đoạn BE
Cho tam giác abc vuông tại A. a) tính độ dài BC, biết AB=4cm , AC=3cm b) So sánh các góc của tam giác ABC Giúp tuoi với 😭
a.Áp dụng định lý pitago vào tam giác ABC vuông tại A, có:
\(BC^2=AB^2+AC^2\)
\(BC^2=4^2+3^2\)
\(BC^2=25\)
\(BC=\sqrt{25}=5\left(cm\right)\)
b.Ta có: \(BC>AB>AC\)
\(\Rightarrow\widehat{A}>\widehat{C}>\widehat{B}\)
a) ...pitago vào tam giác abc vuông tại a
bc^2= ac^2+ab^2
bc^2= 25
bc=5cm
Cho tam giác ABC vuông tại A có AB =9cm , AC=12cm . Đường trung tuyến AM
a. Tính Bc và AM
b. Trên tia đối của tia AC lấy điểm D sao cho AD= AC. CMR tam giác ABC =tam giác ABD từ đó suy ra tam giác BCD là tam giác gì vì sao
c. Gọi M là giao điểm của AD và DM gọi N là trung điểm của BD . CMR C , G , N thẳng hàng
😭😭😭😭😭
Mình cần gấp ạ , mai mình kiểm tra một tiết mà ko làm xong cái này chỉ có lên bàn thờ ngồi với tổ tiên :((((( bạn nào giúp với ạ để mình tick cho 2 lần mình có 2 nick mà yên tâm nha
tự làm là hạnh phúc của mỗi công dân
Tam giác ABC cân tại A, vẽ AH vuông góc BC
a) Chứng minh tam giác ABH = tam giác ACH và H là trung điểm của BC
b) gọi E là trung điểm AB. CE cắt AH tại I. Chứng minh 2(AH+CE) > 3AB
giúp mình với, mình cần gấp😭😭😭
OwO.Thiệt ra iem mới lớp 5 hà ==
Cho tam giác ABC vuông tại A, đường cao AH. Vẽ đường tròn (A ; AH). Kẻ các tiếp tuyến BD, CE với đường tròn (D, E là các tiếp điểm khác H). .a, tính AH b,Cm BD+EC=BC c,cm tứ giác AHCE nội tiếp Mk cần gấp lắm ai làm được mk cảm ơn trước nha 😭😭😭😭😭
b: Xét (A) có
CH,CE là tiếp tuyến
=>CH=CE
Xét (A) có
BH,BD là tiếp tuyến
=>BH=BD
BC=BH+CH
=>BC=BD+CE
c: Xét tứ giác AHCE có
góc AHC+góc AEC=180 độ
=>AHCE nội tiếp
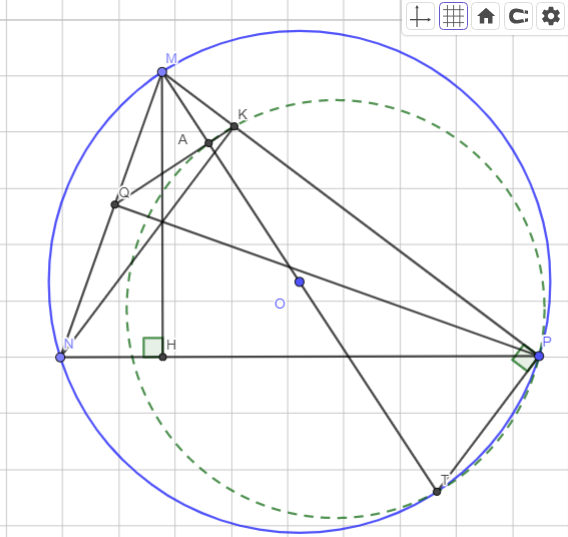
Cho tam giác MNP nhọn nội tiếp (O) có MN < MP. Vẽ các đường cao MH, NK, PQ, đường kính MT. Chứng minh a) MN.MP=MH.MT b) Tứ giác NQKP nội tiếp c) MT vuông góc với KQ (Bạn nào rảnh giúp mình giải với 😭😭 mình đang cần gấp lắm ạ!!!)
Xét $\Delta MNH$ và $\Delta P$ ta có:
$\large \widehat{MHN}=\widehat{MPT}=90^o$
$\large \widehat{MNP}=\widehat{MTP}$(Hai góc cùng chắn cung $MP$)
Do đó $\large \Delta MNH \sim \Delta MTP$ $(g-g)$
Từ đó: $\frac{MN}{MT}=\frac{MH}{MP}\Leftrightarrow MN.MP=MH.MT$
Xét tứ giác $NQKP$ ta có:
$\large \widehat{NQP}=\widehat{PKN}=90^o$
Mà hai góc này cùng chắn cung $NP$
Do đó tứ giác $NQKP$ là tứ giác nội tiếp
Suy ra: $\large \widehat{PKQ}+\widehat{PNQ}=180^o$ (Hai góc nội tiếp đối nhau)
Đồng thời ta có $\large \widehat{PKQ}+\widehat{MKQ}=180^o\Rightarrow \widehat{MNP}=\widehat{MTP}=\widehat{MKQ}$
Gọi $A$ là giao điểm của $QK$ và $MT$
Xét tứ giác $TPKA$ ta có:
$\large \widehat{MTP}+\widehat{PKQ}=\widehat{PKQ}+\widehat{MKQ}=180^o$
Mà hai góc này ở vị trí đối nhau nên tứ giác $TPAK$ là tứ giác nội tiếp
$\large \Leftrightarrow \widehat{MPT}+\widehat{TAK}=180^o\Leftrightarrow \widehat{TAK}=180^o-\widehat{MPT}=90^o$
Do đó $MT$ vuông góc với $QK$
Hình:
Cho tam giác ABC có ba góc nhọn. Gọi I là trung điểm của AC. Trên tia đối của tia ib lấy điểm d sao cho cho ID bằng Ib
A, chứng minh tam giác ABC bằng tam giác cid
B, chứng minh AB song song CD
C, qua c vẽ đường thẳng song song với BD cắt tia AB tại k. Chứng minh bK bằng C d
CẦN GẤP 😭😭😭
Cho tam giác ABC cân tại A, góc A bằng 50 độ. Tính số đo các góc ở đáy của tam giác ABC
Giúp Mình với cảm ơn ạ
Xét \(\Delta\)\(ABC \) ta có : \(\widehat{A}\) + \(\widehat{B}\) + \(\widehat{C}\) = \(180 \)o
⇒\(\widehat{B}\) + \(\widehat{C}\) =\(180 \)o - \(\widehat{A} \)
⇒\(\widehat{B} + \widehat{C} = 130\)o
Vì \(\Delta\)\(ABC\) cân tại A
⇒ \(\widehat{B}=\widehat{C} = 130\)o\(: 2 = 65\)o
*Cách khác:
Ta có: ΔABC cân tại A(gt)
nên \(\widehat{B}=\dfrac{180^0-\widehat{A}}{2}\)(Số đo của các góc ở đáy trong ΔABC cân tại A)
\(\Leftrightarrow\widehat{B}=\dfrac{180^0-50^0}{2}=65^0\)
mà \(\widehat{B}=\widehat{C}\)(hai góc ở đáy trong ΔABC cân tại A)
nên \(\widehat{C}=65^0\)
Vậy: \(\widehat{B}=65^0\); \(\widehat{C}=65^0\)
Cho tam giác ABC có góc B = 90 độ, AC=2AB. Kẻ tia phân giác AE của góc A ( E thuộc BC ), D là trung điểm của AC.
a/ chứng minh ED vuông góc AC
b/ Chứng minh EA=AC
c/ tính các góc BAC và BCA của tam giác ABC
giúp mik với ạ gấp lắm
a: Xét ΔABE và ΔADE có
AB=AD
\(\widehat{BAE}=\widehat{DAE}\)
AE chung
Do đó: ΔABE=ΔADE
Suy ra: \(\widehat{ABE}=\widehat{ADE}\)
hay DE\(\perp\)AC