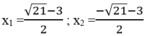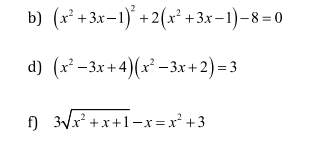
b: \(\Leftrightarrow\left(x^2+3x-1\right)^2+4\left(x^2+3x-1\right)-2\left(x^2+3x-1\right)-8=0\)

\(\Leftrightarrow\left(x^2+3x-1\right)\left(x^2+3x-1+4\right)-2\left(x^2+3x-1+4\right)=0\)

\(\Leftrightarrow x^2+3x-3=0\)

\(\Delta=3^2-4\cdot1\cdot\left(-3\right)=9+12=21>0\)

Do đó: Phương trình có hai nghiệm phân biệt là:

\(\left\{{}\begin{matrix}x_1=\dfrac{-3-\sqrt{21}}{2}\\x_2=\dfrac{-3+\sqrt{21}}{2}\end{matrix}\right.\)

d: \(\Leftrightarrow\left(x^2-3x\right)^2+6\left(x^2-3x\right)+8=3\)

\(\Leftrightarrow\left(x^2-3x\right)^2+5\left(x^2-3x\right)+\left(x^2-3x\right)+5=0\)

\(\Leftrightarrow x^2-3x+1=0\)

\(\Delta=\left(-3\right)^2-4\cdot1\cdot1=5>0\)

Do đó: Phương trình có hai nghiệm phân biệt là:

\(\left\{{}\begin{matrix}x_1=\dfrac{3-\sqrt{5}}{2}\\x_2=\dfrac{3+\sqrt{5}}{2}\end{matrix}\right.\)

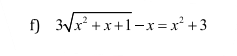
Đặt \(\sqrt{x^2+x+1}=a\)

Pt trở thành \(3a=a^2+2\)

=>(a-1)(a-2)=0

\(\Leftrightarrow\left\{{}\begin{matrix}x^2+x+1=1\\x^2+x+1=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2+x=0\\\left(x+\dfrac{1}{2}\right)^2=\dfrac{13}{4}\end{matrix}\right.\)

\(\Leftrightarrow x\in\left\{0;-1;\dfrac{\sqrt{13}-1}{2};\dfrac{-\sqrt{13}-1}{2}\right\}\)

Đặt m = x - 1 .Điều kiện : m ≥ 0, x  ≥  1

Ta có : x -  x - 1 -3 = 0 ⇔ (x -1) - x - 1  -2 =0

⇔  m 2  -m - 2 =0

Phương trình  m 2  -m - 2 = 0 có hệ số a = 1, b = -1 , c = -2 nên có dạng

a – b + c = 0

Suy ra :  m 1  = -1 (loại) ,  m 2  = -(-2)/1 = 2

Với m =2 ta có: x - 1  =2 ⇒ x -1 =4 ⇔ x =5

Giá trị của x thỏa mãn điều kiện bài toán

Vậy phương trình đã cho có 1 nghiệm : x=5

Đặt m = x/(x+1) .Điều kiện : x ≠ -1

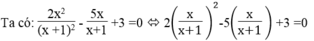
⇔ 2 m 2  -5m +3 =0

Phương trình 2m2 -5m +3 = 0 có hệ số a = 2, b = -5 , c = 3 nên có dạng

a +b + c = 0

suy ra : m 1  = 1 , m 2  =3/2

Với  m 1  =1 ta có: x/(x+1) =1 ⇔ x =x+1 ⇔ 0x =1 (vô nghiệm)

Với m = 3/2 ta có: x/(x+1) = 3/2 ⇔ 2x =3(x +1)

⇔ 2x =3x +3 ⇔ x =-3

Giá trị của x thỏa mãn điều kiện bài toán

Vậy phương trình đã cho có 1 nghiệm : x=-3

ĐKXĐ : \(1\le x\le3\)

\(x-\sqrt{x-1}-3=0\)

\(\Leftrightarrow\left(x-1\right)-\sqrt{x-1}-2=0\)

Đặt \(t=\sqrt{x-1},t\ge0\), suy ra pt trên trở thành \(t^2-t-2=0\Leftrightarrow\left(t-2\right)\left(t+1\right)=0\Leftrightarrow\orbr{\begin{cases}t=2\left(\text{nhận}\right)\\t=-1\left(\text{loại}\right)\end{cases}}\)

Với t = 2 suy ra x = 5

đặt 1/2x-y là a

1/x+y là b

hpt ta đc:

3.a-6.b=1

a-b=0

( giải đi pạn)

Đặt m =4x -5

Ta có:  4 x - 5 2  – 6(4x -5) +8 =0 ⇔ m 2  -6m +8 =0

∆ ’ = - 3 2 -1.8 =9 -8=1 > 0

∆ ' = 1 = 1

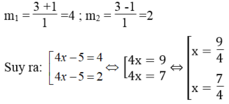
Vậy phương trình đã cho có 2 nghiệm x 1  =9/4 , x 2  =7/4

Đặt m = 2 x 2  +x -2

Ta có: 2 x 2 + x - 2 2 +10 x 2  +5x -16 =0

⇔  2 x 2 + x - 2 2 +5(2 x 2  +x -2) -6 =0

⇔  m 2  +5m -6 =0

Phương trình  m 2  +5m -6 = 0 có hệ số a = 1, b = 5, c = -6 nên có dạng

a + b + c = 0

Suy ra :  m 1  =1 , m 2  =-6

m1 =1 ta có: 2 x 2  +x -2 =1 ⇔ 2 x 2  +x -3=0

Phương trình 2 x 2  +x -3 = 0 có hệ số a = 2, b = 1 , c = -3 nên có dạng

a +b+c=0

Suy ra:  x 1  =1 , x 2  =-3/2

Với m=-6 ta có: 2 x 2  +x -2 = -6 ⇔ 2 x 2  +x +4 =0

∆  =  1 2  -4.2.4 = 1 -32 = -31 < 0 . Phương trình vô nghiệm

Vậy phương trình đã cho có 2 nghiệm :  x 1  =1 , x 2  =-32

Đặt m =  x 2  +3x -1

Ta có:  x 2 + 3 x - 1 2  +2( x 2  +3x -1) -8 =0 ⇔  m 2  +2m -8 =0

∆ ’ = 1 2  -1.(-8) =1 +8 =9 > 0

∆ ' = 9  =3

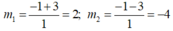
Với m = 2 thì :  x 2 +3x - 1 = 2 ⇔  x 2  + 3x - 3 = 0

∆ ’ =  3 2  -4.1.(-3 )=9 +12=21 > 0

∆ ' = 21

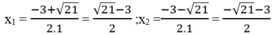
Với m = -4 ta có:  x 2  +3x -1 = -4 ⇔  x 2  +3x +3 = 0

∆  =  3 2  -4.1.3=9 -12 = -3 < 0

Phương trình vô nghiệm

Vậy phương trình đã cho có 2 nghiệm :