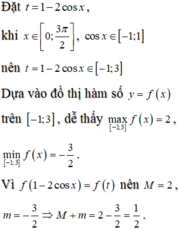Tìm giá trị nhỏ nhất và giá trị x tương ứng của M = |x - 2017| + |x - 17|

Những câu hỏi liên quan
tìm giá trị nhỏ nhất và giá trị x tương ứng A=\(\frac{\left(x-2017\right)+2018}{\left(x-2017\right)+2019}\)
Gọi M, m tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y
2
cos
x
+
1
cos
x
-
2
. Khi đó ta có: A. 9M + m 0 B. 9M - m 0 . C. M + 9m 0 D. M + m 0 .
Đọc tiếp
Gọi M, m tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2 cos x + 1 cos x - 2 . Khi đó ta có:
A. 9M + m = 0
B. 9M - m = 0 .
C. M + 9m = 0
D. M + m = 0 .
Tìm giá trị nhỏ nhất của biểu thức:
A= /x-2010/ + (y+2011) 2010 +2011 và giá trị của x, y tương ứng
vì |x-2010|\(\ge\)0
(y+2011) 2010\(\ge\)0
=>|x-2010|+(y+2011) 2010\(\ge\)0
=>A=|x-2010| + (y+2011) 2010 +2011 \(\ge\)0+2011
dấu "=" xảy ra khi |x-2010|=(y+2011)2010=0
<=>x=2010 và y=-2011
vậy Amin=2011 khi x=2010 và y=-2011
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của:
Q= |x - 2010| + ( y + 2011 )^2010 + 2011
Và các giá trị x,y tương ứng
\(Q=\left|x-2010\right|+\left(y+2011\right)^{2010}+2011\)
Ta có:\(\hept{\begin{cases}\left|x-2010\right|\ge0\\\left(y+2011\right)^{2010}\ge0\end{cases}}\)
Nên \(\left|x-2010\right|+\left(y+2011\right)^{2010}+2011\ge2011\)
Vậy \(Q_{min}=2011\Leftrightarrow\hept{\begin{cases}x-2010=0\\y+2011=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=2010\\y=-2011\end{cases}}\)
Đúng 0
Bình luận (0)
Cho hàm số yf(x) liên tục trên
ℝ
và có đồ thị như hình vẽ. Gọi M và m tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y f(1-2cos x) trên
0
;
3
π
2
. Giá trị của M + m bằng A. 2 B. 1 C.
1
2
D.
3
2
Đọc tiếp
Cho hàm số y=f(x) liên tục trên ℝ và có đồ thị như hình vẽ. Gọi M và m tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f(1-2cos x) trên 0 ; 3 π 2 . Giá trị của M + m bằng
A. 2
B. 1
C. 1 2
D. 3 2
Tìm giá trị nhỏ nhất của biểu thức M=\(\sqrt{x^2+2x+5}\) và giá trị tương ứng của \(x\)
\(\sqrt{\left(x^2+2x+1\right)+4}=\sqrt{\left(x+1\right)^2+4}\supseteq\sqrt{4}=2\)
=> min M=2 => x=-1
Đúng 0
Bình luận (0)
\(\sqrt{x^2+2x+5}\)
Tìm giá trị nhỏ nhất của biểu thức và giá trị tương ứng của x
\(\sqrt{x^2+2x+5}=\sqrt{\left(x+1\right)^2+4}\ge\sqrt{4}=2.\)với mọi x
GTNN \(\sqrt{x^2+2x+5}=2\)khi x = -1
Đúng 0
Bình luận (0)
\(\sqrt{x^2+2x+5}=\sqrt{\left(x+1\right)^2+4}\ge2\) với x=-1
Đúng 0
Bình luận (0)
a) Tìm giá trị nhỏ nhất của biểu thức : "B=I x+11 I + I 1-y I + 2017 "và cho biết giá trị của "x , y" để "B" đạt giá trị nhỏ nhất.
Để B nhỏ nhất nên | x + 11| = 0 và | 1 -y | = 0
Với | x + 11 | = 0 thì x + 11 = 0 nên x = -11
Với | y - 1 | = 0 thì y - 1 = 0 nên y =1
Vậy x = -11 , y =1
hok tốt
Đúng 1
Bình luận (2)
\(B=\left(x+\frac{2}{3}\right)^2+5\). Tìm giá trị nhỏ nhất của B và giá trị tương ứng của x.