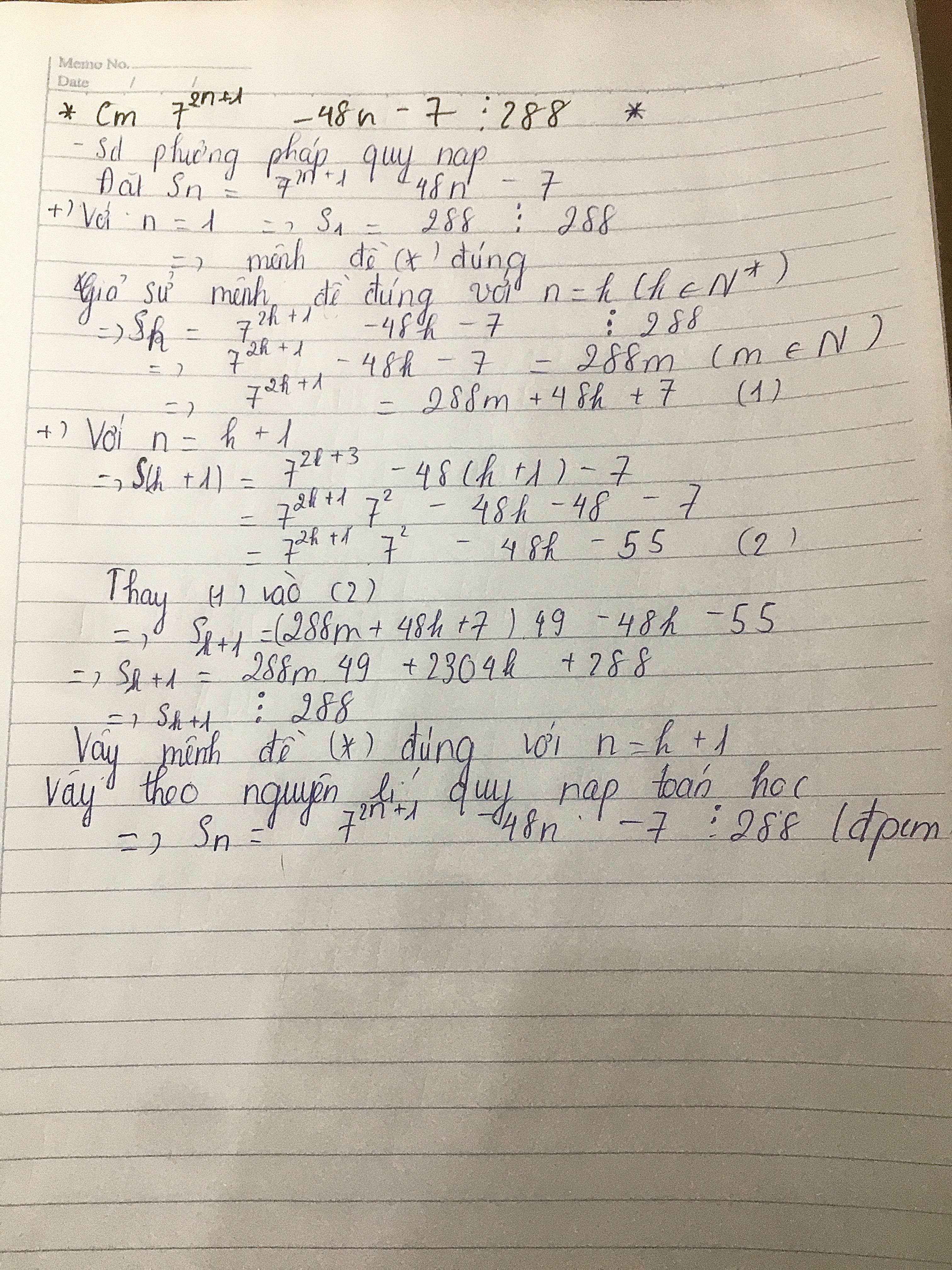cm 7^2n-48n-1 chia hết cho 2304

Những câu hỏi liên quan
cm 7^2n-48n-1 chia hết cho 2304
CMR: 7^2n+1 - 48n-7 chia hết cho 288
7^(2n+1) -48n -7 chia hết cho 288 (1)
Đặt S(n) = 7^(2n+1) - 48n -7
Với n =0 thì S(0) = 7^1 -7 =0 chia hết cho 288
Vậy (1) đúng với n =0
Giả sử (1) đúng với n= k (k thuộc N* ) tức là:
S(k) = 7^(2k+1) -48k -7 chia hết cho 288
Ta cần C/m (1) đúng với n= k+1, nghĩa là phải C/m:
S( k+1) = 7^[2(k+1) +1) ] -48(k+1) -7 chia hết cho 288
Thật vậy ta có:
S(k+1) = 7^(2k+3) -48k - 48- 7
= 7^(2k+1). 49 - 48.49k +2304k -55
= 49. ( 7^(2k+1) - 48k - 7) +2304k +288
= 49.S(k) + 2304k +288
Theo giả thiết quy nạp thì S(k) chia hết cho 288
Mà 2304k và 288 cũng chia hết cho 288
nên S(k+1) chia hết cho 288 (đpcm)
Đúng 0
Bình luận (0)
CMR 7^2n . 7 -48n -7 chia hết cho 288 ( n thuộc N)
chứng minh rằng: \(7^{2n+1}-48n-7\)chia hết cho 288 với mọi n thuộc N
chứng minh ràng:
\(7^{2n+1}-48n-7\)chia hết cho 288 với mọi n thuộc N
Mình chứng minh theo phương pháp quy nạp
- Với n=1 thì phương trình ra 288 sẽ chia hết 288
- Với n=k => 7 -48k - 7 chia hết 288
Chứng minh với n=k+1 thì đẳng thức chia hết 288
Thế n bằng k+1
=
Vì chia hết 288 ( chứng minh phần n=k)
2304 chia hết 288 => 2304k chia hết 288
288 thì chia hết 288
=> đẳng thức đúng với n=k+1
=> Dpcm
Đúng 0
Bình luận (0)
CM: n3- 48n chia hết cho 48 với mọi n chẵn
Thử với n = 2 thì đề sai, mà hình như với mọi n chẵn thì đề sai :v
Chứng Minh \(7^{2n+1}-48n-7⋮288\)
N thuộc z ko chia hết cho 3 .cm P=22n+2n+1 chia hết cho 7
n chia hết cho n-2
n+7 chia hết cho (n+1)
21 chia hết cho 2n+5
2n+7 chia het cho 2n+1
\(n⋮n-2\\ \Rightarrow n-\left(n-2\right)⋮n-2\\ \Rightarrow2⋮n-2\\ \Rightarrow n-2\in\left\{1;2\right\}\\ \Rightarrow n\in\left\{3;4\right\}\)Vậy \(n\in\left\{3;4\right\}\)
\(n+7⋮n+1\\ \Rightarrow n+7-\left(n+1\right)⋮n+1\\ \Rightarrow6⋮n+1\\ \Rightarrow n+1\in\left\{1;2;3;6\right\}\\ \Rightarrow n\in\left\{0;1;2;5\right\}\)Vậy \(n\in\left\{0;1;2;5\right\}\)
\(21⋮2n+5\\ \Rightarrow2n+5\in\left\{1;3;7;21\right\}\\ \Rightarrow2n\in\left\{2;16\right\}\\ \Rightarrow n\in\left\{1;8\right\}\)Vậy \(n\in\left\{1;8\right\}\)
\(2n+7⋮2n+1\\ \Rightarrow2n+7-\left(2n+1\right)⋮2n+1\\ \Rightarrow6⋮2n+1\\ \Rightarrow2n+1\in\left\{1;2;3;6\right\}\\ \Rightarrow2n\in\left\{0;1;2;5\right\}\\ \Rightarrow n\in\left\{0;1\right\}\)Vậy \(n\in\left\{0;1\right\}\)