Cho tan α = 2 . Tính \(\frac{2cos\text{α + sinα}}{sin\text{α - 3 cosα }}\)

Những câu hỏi liên quan
A = \(\dfrac{\text{sinα + cosα}}{\text{sinα - cosα}}\) Tính α biết tan α = \(\sqrt{3}\)
\(A=\dfrac{\dfrac{sina}{cosa}+\dfrac{cosa}{cosa}}{\dfrac{sina}{cosa}-\dfrac{cosa}{cosa}}=\dfrac{tana+1}{tana-1}=\dfrac{\sqrt{3}+1}{\sqrt{3}-1}=2+\sqrt{3}\)
Đúng 1
Bình luận (0)
Tính:\(\frac{3\sin\text{α}+2cos\text{α}}{3sin\text{α}-2cos\text{α}}\) Biết tanα=8
\(A=\frac{\frac{3sina}{cosa}+\frac{2cosa}{cosa}}{\frac{3sina}{cosa}-\frac{2cosa}{cosa}}=\frac{3tana+2}{3tana-2}=\frac{24+2}{24-2}=\frac{26}{22}=\frac{13}{11}\)
Cho góc α
thỏa mãn `π\2`<α<π,cosα=−\(\dfrac{1}{\sqrt{3}}\). Tính giá trị của các biểu thức sau:
a) sin(α+\(\dfrac{\text{π}}{6}\))
b) cos(α+$\frac{\text{π}}{6}$)
c) sin(α−$\frac{\text{π}}{3}$)
d) cos(α−$\frac{\text{π}}{6}$)
a: pi/2<a<pi
=>sin a>0
\(sina=\sqrt{1-\left(-\dfrac{1}{\sqrt{3}}\right)^2}=\dfrac{\sqrt{2}}{\sqrt{3}}\)
\(sin\left(a+\dfrac{pi}{6}\right)=sina\cdot cos\left(\dfrac{pi}{6}\right)+sin\left(\dfrac{pi}{6}\right)\cdot cosa\)
\(=\dfrac{\sqrt{3}}{2}\cdot\dfrac{\sqrt{2}}{\sqrt{3}}+\dfrac{1}{2}\cdot-\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{6}-2}{2\sqrt{3}}\)
b: \(cos\left(a+\dfrac{pi}{6}\right)=cosa\cdot cos\left(\dfrac{pi}{6}\right)-sina\cdot sin\left(\dfrac{pi}{6}\right)\)
\(=\dfrac{-1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}-\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}=\dfrac{-\sqrt{3}-\sqrt{2}}{2\sqrt{3}}\)
c: \(sin\left(a-\dfrac{pi}{3}\right)\)
\(=sina\cdot cos\left(\dfrac{pi}{3}\right)-cosa\cdot sin\left(\dfrac{pi}{3}\right)\)
\(=\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}+\dfrac{1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}=\dfrac{\sqrt{2}+\sqrt{3}}{2\sqrt{3}}\)
d: \(cos\left(a-\dfrac{pi}{6}\right)\)
\(=cosa\cdot cos\left(\dfrac{pi}{6}\right)+sina\cdot sin\left(\dfrac{pi}{6}\right)\)
\(=\dfrac{-1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}+\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}=\dfrac{-\sqrt{3}+\sqrt{2}}{2\sqrt{3}}\)
Đúng 0
Bình luận (0)
Chứng minh các biểu thức sau không phụ thuộc vào α
A=(sinα+cosα)2+(sinα−cosα)2
B=sin4α(1+2cos2α)+cos4α(1+2sin2α)
C=sin4α(3−2sin2α)+cos4α(3−2cos2α)
Giúp tớ điii
\(A=\left(\sin\alpha+\cos\alpha+\sin\alpha-\cos\alpha\right)^2-2\left(\sin\alpha+\cos\alpha\right)\left(\sin\alpha-\cos\alpha\right)\)
\(=4\sin^2\alpha-2\sin^2\alpha+2\cos^2\alpha=2\left(\sin^2\alpha+\cos^2\alpha\right)=2\)
\(B=\sin^4\alpha+\cos^4\alpha+2\sin^2\alpha.\cos^2\alpha\left(\sin^2\alpha+\cos^2\alpha\right)=\sin^4\alpha+\cos^4\alpha+2\sin^2\alpha.\cos^2\alpha\)
\(=\left(\sin^2\alpha+\cos^2\alpha\right)^2-1=0\)
\(C=3\left(\sin^4\alpha+\cos^4\alpha\right)-2\sin^2\alpha.\cos^2\alpha\left(\sin^2\alpha+\cos^2\alpha\right)=3\left(\sin^4\alpha+\cos^4\alpha\right)-2\sin^2\alpha.\cos^2\alpha\)
\(=3\left(\sin^2\alpha+\cos^2\alpha-\frac{1}{9}\right)^2-\frac{1}{9}=\frac{61}{27}\)
Đúng 0
Bình luận (0)
Rút gọn bt
a/A=(sinα +cosα )2 +(sinα-cosα)2
b/ B=(1+tan2α ) (1-sin2α) -(1+cot2α)(1-cos2α)
a/ \(A=\left(sin\alpha+cos\alpha\right)^2+\left(sin\alpha-cos\alpha\right)^2=2\left(sin^2\alpha+cos^2\alpha\right)=2\)
b/ \(B=\left(1+tan^2\alpha\right)\left(1-sin^2\alpha\right)-\left(1+cotg^2\alpha\right)\left(1-cos^2\alpha\right)\)
\(=\left(1+\frac{sin^2\alpha}{cos^2\alpha}\right)\left(1-sin^2\alpha\right)-\left(1+\frac{cos^2\alpha}{sin^2\alpha}\right)\left(1-cos^2\alpha\right)\)
\(=\frac{1}{cos^2\alpha}.cos^2\alpha-\frac{1}{sin^2\alpha}.sin^2\alpha=1-1=0\)
Đúng 0
Bình luận (0)
Cho góc α thỏa mãn
0
α
π
4
và
sin
α
+
cos
α
5
2
. Tính P sinα - cosα A.
P
3
2
B. P 1 C. P -1/2 D.
P
-...
Đọc tiếp
Cho góc α thỏa mãn 0 < α < π 4 và sin α + cos α = 5 2 . Tính P = sinα - cosα
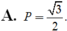 A.
P
=
3
2
A.
P
=
3
2
B. P = 1
C. P = -1/2
D. P = - 3 2
Chọn D.
Ta có ( sinα - cosα) 2 + (sinα + cosα) 2 = 2( sin2α + cos2α) = 2.
Suy ra (sinα - cosα) 2 = 2 - ( sinα + cos α) 2 = 2 - 5/4 = 3/4.
Do ![]() suy ra sinα < cosα nên sinα - cosα < 0.
suy ra sinα < cosα nên sinα - cosα < 0.
Vậy 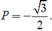
Đúng 0
Bình luận (0)
~Các bạn giúp mk làm bài này nhé! Cảm ơn các bạn nhiều ...~ Bài 1:Tính giá trị biểu thứca) A sin10°+sin20°+sin30°+sin40°-cos50°-cos60°-cos70°-cos80°b) C cos²52° sin45°+sin²52° cos45°c) E sin²5°+sin²15°+sinv25°+sin²35°+sin²45°+sin²55°+sin²65°+sin²75°+sin²85°Bài 2: C/m rằng với góc nhọn α ta luôn cóa) (sinα +cosα)²-(sinα -cosα)² 4sinα cosαb) cosα/1-sinα 1+sinα/cosαc) √̅s̅i̅n̅²̅x̅(̅1̅+̅̅c̅o̅t̅̅x̅)̅̅+̅c̅o̅s̅²̅x̅(̅1̅+̅t̅a̅n̅x̅)̅ sinx+cosxBài 3: Cho α là một góc nhọn a) Biết sinα 3/4. Tính cosα(90°-...
Đọc tiếp
~Các bạn giúp mk làm bài này nhé! Cảm ơn các bạn nhiều ...~
Bài 1:Tính giá trị biểu thức
a) A= sin10°+sin20°+sin30°+sin40°-cos50°-cos60°-cos70°-cos80°
b) C= cos²52° sin45°+sin²52° cos45°
c) E= sin²5°+sin²15°+sinv25°+sin²35°+sin²45°+sin²55°+sin²65°+sin²75°+sin²85°
Bài 2: C/m rằng với góc nhọn α ta luôn có
a) (sinα +cosα)²-(sinα -cosα)² = 4sinα cosα
b) cosα/1-sinα =1+sinα/cosα
c) √̅s̅i̅n̅²̅x̅(̅1̅+̅̅c̅o̅t̅̅x̅)̅̅+̅c̅o̅s̅²̅x̅(̅1̅+̅t̅a̅n̅x̅)̅ =sinx+cosx
Bài 3: Cho α là một góc nhọn
a) Biết sinα =3/4. Tính cosα(90°-α)
b) Biết tanα =2. Tính cotα(90°-α)
cho góc nhọn α :
chứng minh rằng: \(\frac{1-\tan\text{α}}{1+\tan\text{α}}\)=\(\frac{\cos\text{α}-\sin\text{α}}{\cos\text{α}+\sin\text{α}}\)
\(\frac{1-tana}{1+tana}=\frac{1-\frac{sina}{cosa}}{1+\frac{sina}{cosa}}=\frac{\frac{1}{cosa}\left(cosa-sina\right)}{\frac{1}{cosa}\left(cosa+sina\right)}=\frac{cosa-sina}{cosa+sina}\)
Đúng 0
Bình luận (0)
Chứng minh : \(\dfrac{sin^2\text{α}}{cos\text{α}\left(1+tan\text{α}\right)}-\dfrac{cos^2\text{α}}{sin\text{α}\left(1+cot\text{α}\right)}-sin\text{α}-cos\text{α}\)


















