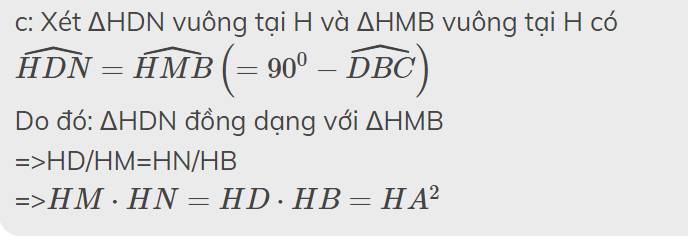cho hình chữ nhật ABCD , kẻ AH vuông góc với BD , biết HD=9cm , HB=16 cm. Tính AB, BC

Những câu hỏi liên quan
Tính AB , AD của hình chữ nhật ABCD biết đường vuông góc AH kẻ từ A đến BD chia đoạn BD thành 2 đoạn thẳng HD=9cm , HB=16cm
Cho hình chữ nhật ABCD, gọi H là chân đường vuông góc hạ từ A xuống BD( AH vuông góc với BD) . Biết HB=9cm, HD=3cm.
Tính độ dài AB, AD
Bài 5. Cho hình chữ nhật ABCD, qua A kẻ đường vuông góc với BD tại H. Biết AB = 20 cm , AH = 12 cm a) Tính AD, HD, HB .b) AH cắt CD tại M. Chứng minh: DH.DB=AH.AM C) AH cắt BC tại K. Chứng minh; HA^ 2 =HM.HK
b: Xét ΔADM vuông tại D có DH là đường cao ứng với cạnh huyền AM
nên \(AH\cdot AM=AD^2\left(1\right)\)
Xét ΔADB vuông tại A có AH là đường cao ứng với cạnh huyền DB
nên \(DH\cdot DB=AD^2\left(2\right)\)
Từ (1) và (2) suy ra \(DH\cdot DB=AH\cdot AM\)
Đúng 0
Bình luận (0)
hình chữ nhật ABCD có AB=8cm AD=6cm kẻ AH vuông góc BD (H thuộc BD)
a) CM tam giác HDA đồng dạng tam giác ADB
b) Tính BD,AH
c) CM BC bình = DH nhân BH
Giải giúp mình cái
d)CM AH bình=HD nhân HB
Cho hình chữ nhật ABCD, AB9cm,AC12cm,kẻ AH vuông góc với BD tại Ha) Tính BD,AH và góc BDAb) Kẻ HI vuông góc AB.CM AI.ABDH.HBc) Đường thẳng AH cắt BC tại M, cắt DC tại N. CM HA2HM.HNgiúp tui giải ik mà làm ơn
Đọc tiếp
Cho hình chữ nhật ABCD, AB=9cm,AC=12cm,kẻ AH vuông góc với BD tại H
a) Tính BD,AH và góc BDA
b) Kẻ HI vuông góc AB.CM AI.AB=DH.HB
c) Đường thẳng AH cắt BC tại M, cắt DC tại N. CM HA2=HM.HN
giúp tui giải ik mà làm ơn![]()
![]()
![]()
a: ΔABD vuông tại A
=>\(BD^2=AB^2+AD^2\)
=>\(BD^2=9^2+12^2=225\)
=>BD=15(cm)
Xét ΔABD vuông tại A có AH là đường cao
nên \(AH\cdot BD=AB\cdot AD\)
=>\(AH\cdot15=12\cdot9=108\)
=>AH=108/15=7,2(cm)
XétΔABD vuông tại A có \(sinBDA=\dfrac{AB}{BD}=\dfrac{9}{15}=\dfrac{3}{5}\)
nên \(\widehat{BDA}\simeq37^0\)
b: Xét ΔAHB vuông tại H có HI là đường cao
nên \(AI\cdot AB=AH^2\left(1\right)\)
Xét ΔABD vuông tại A có AH là đường cao
nên \(AH^2=HD\cdot HB\left(2\right)\)
Từ (1) và (2) suy ra \(AI\cdot AB=HD\cdot HB\)
c: Xét ΔHDN vuông tại H và ΔHMB vuông tại H có
\(\widehat{HDN}=\widehat{HMB}\left(=90^0-\widehat{DBC}\right)\)
Do đó: ΔHDN đồng dạng với ΔHMB
=>HD/HM=HN/HB
=>\(HM\cdot HN=HD\cdot HB=HA^2\)
Đúng 2
Bình luận (1)
Cho hình chữ nhật ABCD, AB9cm,AC12cm,kẻ AH vuông góc với BD tại Ha) Tính BD,AH và góc BDAb) Kẻ HI vuông góc AB.CM AI.ABDH.HBc) Đường thẳng AH cắt BC tại M, cắt DC tại N. CM HA2HM.HNgiúp tui vs tui đag cần lời giải gấp
Đọc tiếp
Cho hình chữ nhật ABCD, AB=9cm,AC=12cm,kẻ AH vuông góc với BD tại H
a) Tính BD,AH và góc BDA
b) Kẻ HI vuông góc AB.CM AI.AB=DH.HB
c) Đường thẳng AH cắt BC tại M, cắt DC tại N. CM HA2=HM.HN
giúp tui vs tui đag cần lời giải gấp ![]()
![]()
![]()
cho hình chữ nhật ABCD, AH vuông góc với BD (H thuộc BD), HD = 2cm, HB = 6cm. tính dộ dài AB, AD
hình bạn tự vẽ nha
áp dụng định lý py ta go vào tam giác ABD ta có AD^2 + AB^2 =64 (1)
áp dụng định lý pytago vào tam giác ABH ta có AB^2 = AH^2+ 36 (2)
áp dụng định lý pytago vào tam giác AHD ta có AD^2= AH^2 +4 (3)
thay (2)và (3) vào (1)
ta có 2AH^2 =24
=> AH^2 =12
thay AH^2=12 lần lượt vào 2 và 3
=> AB^2=12+36=48=>AB=\(\sqrt{48}\)
AD^2=12+4=16 => AD=4
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A .kẻ AH vuông góc với BC . biết HB = 9cm,HC =16 cm;AC=5cm . tính AH;AB
TA CÓ BH + HC = BC
=> BC = 9+16=25
THEO ĐỊNH LÝ PITAGO XÉT \(\Delta ABC\)VUÔNG TẠI A CÓ
\(BC^2=AB^2+AC^2\)
\(AB^2=BC^2-AC^2\)
\(AB^2=25^2-5^2\)
......
AH TƯƠNG TỰ
Cho hình chữ nhật ABCD có AB = 12cm, BC = 9cm. Kẻ AH vuông góc với BD. a) Chứng minh: HBA đồng dạng ABC b) Tính độ cao AH c) Tính dIện tích AHB
Áp dụng định lý pitago: \(AC=\sqrt{12^2+9^2}=\sqrt{225}=15\left(cm\right)\)
Xét tam giác HBA và tam giác ABC, có:
\(\widehat{BHA}=\widehat{ABC}=90^o\)
\(\widehat{A}\): chung
Vậy tam giác HAB đồng dạng tam giác BAC ( g.g )
\(\Rightarrow\dfrac{AH}{AB}=\dfrac{AB}{AC}=\dfrac{HB}{BC}\)
\(\Rightarrow AH=\dfrac{AB^2}{AC}=\dfrac{12^2}{15}=9,6\left(cm\right)\)
\(\Rightarrow HB=\dfrac{AB.BC}{AC}=\dfrac{12.9}{15}=7,2\left(cm\right)\)
\(S_{AHB}=\dfrac{1}{2}.AH.HB=\dfrac{1}{2}.9,6.7,2=34,56\left(cm^2\right)\)
Đúng 7
Bình luận (2)
a,
Xét Δ HBA và Δ BAC, có :
\(\widehat{BHA}=\widehat{ABC}=90^o\)
\(\widehat{ABH}=\widehat{CAB}\) (cùng phụ \(\widehat{ABC}\))
=> Δ HBA ~ Δ BAC (g.g)
Đúng 4
Bình luận (0)
b,
Xét Δ ABC vuông tại B, có :
\(AC^2=AB^2+BC^2\) (Py - ta - go)
=> \(AC^2=12^2+9^2\)
=> AC = 15 (cm)
Ta có : Δ HBA ~ Δ BAC (cmt)
=> \(\dfrac{HA}{BC}=\dfrac{BA}{AC}\)
=> \(\dfrac{HA}{9}=\dfrac{12}{15}\)
=> HA = 7,2 (cm)
c,
Xét Δ AHD vuông tại H, có :
\(AD^2=AH^2+DH^2\) (Py - ta - go)
=> \(9^2=7,2^2+DH^2\)
=> DH = 5,4 (cm)
Ta có : BD = BH + DH
=> 15 = BH + 5,4
=> BH = 9,6 (cm)
Ta có :
\(S_{\text{Δ}AHB}=\dfrac{1}{2}.AH.HB\)
=> \(S_{\text{Δ}AHB}=34,56\left(cm^2\right)\)
Đúng 1
Bình luận (0)