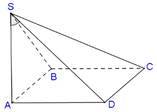
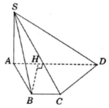
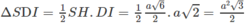Chủ đề / Chương

Bài học

Hãy tham gia nhóm Học sinh Hoc24OLM
Bạn chưa đăng nhập. Vui lòng đăng nhập để hỏi bài
Mai Thị Hà Châu
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, Sa vuông góc với mặt phẳng đáy và SA 2a. Biết góc giữa Sd và mặt phẳng (SAC) bằng 300 . Tính thể tích khối chóp S.ABCDA. VS.ABCD  frac{2a^3}{3}                      B. VS.ABCD  frac{a^3}{3}                     C. VS.ABCD  frac{a^3sqrt{3}}{3}                   D. VS.ABCD  frac{a^3sqrt{6}}{3} 
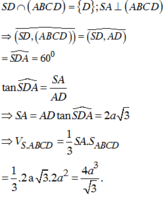
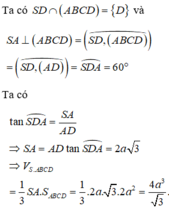
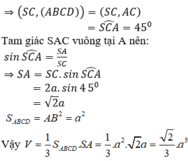
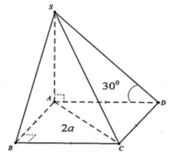
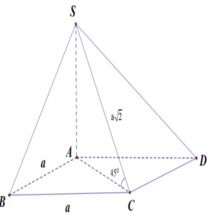
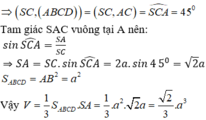
Đọc tiếp
Lớp 12 Toán
Những câu hỏi liên quan
Pham Trong Bach
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh ABa; AD2a cạnh bên SA vuông góc với mặt phẳng đáy, góc giữa SD và mặt phẳng đáy bằng 60 độ Thể tích V của khối chóp S.ABCD là A.  V 2 a 3 3 B.  V 4 a 3 3 C. ...
Đọc tiếp
Xem chi tiết
Lớp 0 Toán

Khách
 
Cao Minh Tâm
Cao Minh Tâm
10 tháng 2 2019 lúc 6:07

Chọn đáp án D.

Bình luận (0)
Pham Trong Bach
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 2a. Biết SA6a và SA vuông góc với mặt phẳng đáy. Tính thể tích khối chóp S.ABCD
Đọc tiếp
Xem chi tiết
Lớp 12 Toán

Khách
 
Cao Minh Tâm
Cao Minh Tâm
10 tháng 12 2019 lúc 6:15

Bình luận (0)
Pham Trong Bach
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình chữ nhật, cạnh A B a , A D 2 a ,  cạnh bên SA vuông góc với mặt phẳng đáy, góc giữa cạnh SD và mặt phẳng đáy bằng 60 o . Thể tích V của khối chóp S.ABCD là A.  V 2 a 3...
Đọc tiếp
Xem chi tiết
Lớp 0 Toán

Khách
 
Cao Minh Tâm
Cao Minh Tâm
4 tháng 10 2019 lúc 6:53

 Đáp án D

Bình luận (0)
Pham Trong Bach

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy, góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng 45° và SC = 2a. Tính thể tích V của khối chóp S.ABCD.

Xem chi tiết
Lớp 12 Toán

Khách
 
Cao Minh Tâm
Cao Minh Tâm
21 tháng 11 2019 lúc 11:22

Vì SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD).

Bình luận (0)
Pham Trong Bach
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, cạnh SA vuông góc với đáy và cạnh AC2a. Góc giữa hai mặt phẳng (SCD) và (ABCD) bằng 30°. Thể tích khối chóp S.ABCD là A.   a 3 3 6 B.  2 a 3 6 9...
Đọc tiếp
Xem chi tiết
Lớp 0 Toán

Khách
 
Cao Minh Tâm
Cao Minh Tâm
19 tháng 4 2017 lúc 7:09

Bình luận (0)
Pham Trong Bach

Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy, góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng 45° và SC = 2a. Tính thể tích V của khối chóp S.ABCD.

Xem chi tiết
Lớp 12 Toán

Khách
 
Cao Minh Tâm
Cao Minh Tâm
9 tháng 5 2017 lúc 10:07

Vì SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD).

Bình luận (0)
Pham Trong Bach
Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng đáy. ABCD là hình vuông có đường chéo AC 2a. Biết rằng tam giác SAC vuông cân. Tính thể tích khối chóp S.ABC?
Đọc tiếp
Xem chi tiết
Lớp 12 Toán

Khách
 
Cao Minh Tâm
Cao Minh Tâm
11 tháng 10 2017 lúc 4:56

Đáp án D

Bình luận (0)
Pham Trong Bach
Hình chóp S.ABCD có đáy là hình thang vuông ABCD vuông tại A và D, có AB 2a, AD DC a, có cạnh SA vuông góc với mặt phẳng (ABCD) và SA a.a) Chứng minh mặt phẳng (SAD) vuông góc với mặt phẳng (SDC), mặt phẳng (SAC) vuông góc với mặt phẳng (SCB).b) Gọi φ là góc giữa hai mặt phẳng (SBC) và (ABCD), tính tanφ.c) Gọi (α) là mặt phẳng chứa SD và vuông góc với mặt phẳng (SAC). Hãy xác định (α) và xác định thiết diện của hình chóp S.ABCD với (α)
Đọc tiếp
Xem chi tiết
Lớp 11 Toán

Khách
 
Cao Minh Tâm
Cao Minh Tâm
21 tháng 7 2019 lúc 4:55

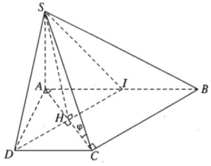
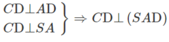
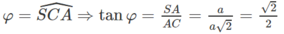
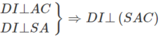
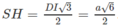Giải sách bài tập Toán 11 | Giải sbt Toán 11

a) Ta có:

Giải sách bài tập Toán 11 | Giải sbt Toán 11

⇒ (SCD) ⊥ (SAD)

Gọi I là trung điểm của đoạn AB. Ta có AICD là hình vuông và IBCD là hình bình hành. Vì DI // CB và DI ⊥ CA nên AC ⊥ CB. Do đó CB ⊥ (SAC).

Vậy (SBC) ⊥ (SAC).

b) Ta có:

Giải sách bài tập Toán 11 | Giải sbt Toán 11

c) Giải sách bài tập Toán 11 | Giải sbt Toán 11

Vậy (α) là mặt phẳng chứa SD và vuông góc với mặt phẳng (SAC) chính là mặt phẳng (SDI). Do đó thiết diện của (α) với hình chóp S.ABCD là tam giác đều SDI có chiều dài mỗi cạnh bằng a√2. Gọi H là tâm hình vuông AICD ta có SH ⊥ DI và Giải sách bài tập Toán 11 | Giải sbt Toán 11 .

Tam giác SDI có diện tích:

Giải sách bài tập Toán 11 | Giải sbt Toán 11

Bình luận (0)
Pham Trong Bach
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a,SA vuông góc với đáy, SD tạo với mặt phẳng (SAB) một góc bằng 60 0 .  Tính thể tích V của khối chóp S.ABCD. A. 4 3 a 3 3 . B. 8 3...
Đọc tiếp
Xem chi tiết
Lớp 0 Toán

Khách
 
Cao Minh Tâm
Cao Minh Tâm
15 tháng 2 2019 lúc 16:19

Đáp án B

Ta có

A D ⊥ A B A D ⊥ S A ⇔ A D ⊥ S A B .

Vậy  S D , S A B = S D , S A = A S D ^ = 60 0 .

Trong tam giác vuông SAD ta có 

Vậy thể tích khối chóp S.ABCD bằng  S A = A D . cot A S D ^ = 2 a 3 . V S A B C D = 1 3 S A B C D . S A = 1 3 4 a 2 . 2 a 3 = 8 3 a 3 9 .

Bình luận (0)
Pham Trong Bach
Cho hình chóp S.ABCD có đáy ABCD là hình thang cân với cạnh đáy AD và BC. AD 2a,AB BC CD a, B A D ⏞ 60 o . Cạnh bên SA vuông góc với mặt phẳng (ABCD) và SD tao với mặt phẳng (ABCD) góc 45 o . Tính theo a thể tích V của khối chóp S.ABCD...
Đọc tiếp
Xem chi tiết
Lớp 12 Toán

Khách
 
Cao Minh Tâm
Cao Minh Tâm
31 tháng 1 2018 lúc 1:51

Đáp án B.

Hướng dẫn giải:Ta có

Suy ra tam giác SAD vuông cân tại A nên SA = AD =2a .

Trong hình thang ABCD , kẻ B H ⊥ A D ( H ∈ A D ) .

Do ABCD là hình thang cân nên A H = A D - B C 2 = a 2 .

Tam giác AHB ,có  B H = A B 2 - A H 2 = a 3 2

Diện tích S A B C D = 1 2 ( A D + B C ) . B H = 3 a 3 2 4  .

Vậy   V S . A B C D = 1 3 S A B C D . S A = a 3 3 2

Bình luận (0)