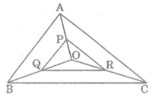
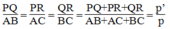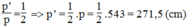Cho O là một điểm nằm trong tam giác ABC có chu vi bằng 2p. CMR p < OA + OB + OC < 2p

Những câu hỏi liên quan
a) M là 1 trung điểm trong \(\Delta ABC\) . CMR AM+BM<BC+AC
b) O là điểm nằm trong \(\Delta ABC\)có chu vi bằng 2P. CMR P<OA+OB+OC<2P
Bạn nào thông minh giúp tớ bài này vs:
Cho tam giác ABC có chu vi bằng 2P. O là một điểm thuộc tam giác ABC. CMR P < OA+OB+OC < 2P
_chú ý: P là nửa chu vi; 2P chu vi
Xem chi tiết
Gọi \(\left\{D\right\}=AO\cap BC\)
\(\Delta BOC:OB+OC>BC\) (1)
\(\Delta AOC:OA+OC>AC\) (2)
\(\Delta AOB:OA+OB>AB\) (3)
Từ (1), (2), (3)\(\Rightarrow2\left(OA+OB+OC\right)>AB+AC+BC\)
\(\Rightarrow OA+OB+OC>\dfrac{2P}{2}=P\) (4)
\(\Delta ACD:AC+DC>AD=AO+OD\) (5)
\(\Delta BOD:BD+OD>BO\) (6)
Từ (5), (6)\(\Rightarrow AC+BD+DC+OD>AO+BO+OD\)
\(\Rightarrow AC+BC>AO+BO\) (7)
Chứng minh tương tự ta được:
AB+BC>AO+CO (8)
AB+AC>BO+CO (9)
Từ (7),(8) ,(9)\(\Rightarrow2\left(AB+AC+BC\right)>2\left(OA+OB+OC\right)\)
\(\Rightarrow AB+AC+BC=2P>OA+OB+OC\) (10)
Từ (4), (10)\(\Rightarrow P< OA+OB+OC< 2P\)
Chúc bạn học tốt![]()
Đúng 0
Bình luận (2)
cho tam giác ABC có chu vi 20cm . Gọi O là một điểm nằm trong tam giác : D ; E ; F lần lượt là trung điểm của OA ; OB ; OC . Tính chu vi tam giác DEF.
Ta có: D; E lần lượt là trung điểm của OA; OB
=> DE là đường trung bình của tam giác OAB
=> DE = 1/2 AB
Chứng minh tương tự: DF = 1/2 AC; EF = 1/2 BC
=> DE + DF + EF = 1/2 AB + 1/2 AC + 1/2 BC = 1/2 (AB + AC + BC) = 1/2 . 20 = 10 cm
gọi O là điểm bất kì nằm trong tam giác ABC. CMR:
a, OB+OC < AB+AC
b, OA+OB + OC > nửa chu vi nhung <chu vi cu tam giá ABC
Cho tam giác ABC và điểm O nằm trong tam giác đó. Gọi P, Q, R lần lượt là trung điểm của các đoạn thẳng OA, OB, OC. Tính chu vi của tam giác PQR, biết rằng tam giác ABC có chu vi p bằng 543 cm.
Cho tam giác ABC và điểm O nằm trong tam giác. Gọi M, N, P lần lượt là trung điểm của OA, OB, OC. Biết chu vi tam giác ABC bằng 10cm. Tính chu vi tam giác MNP. Chu vi tam giác MNP: cm
Xét tam giác PAC,ta có:
{MP=MAOP=OC
=>MP = 1/2 AC
Tam giác PBC và AOB tương tự
=> Tam giác MNP đồng dạng với tam giác ABC
=> Chu vi tam giác MNP = 543/2 cm
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC và một điểm O nằm trong tam giác đó. Gọi P, Q, R lần lượt là trung điểm của các đoạn thẳng OA, OB, OC.a) Chứng minh
Δ
P
Q
R
∽
Δ
A
B
C
.b) Cho biết
Δ
A
B
C
có chu vi bằng 543cm, hãy tính chu vi
Δ
P
Q
R
.
Đọc tiếp
Cho tam giác ABC và một điểm O nằm trong tam giác đó. Gọi P, Q, R lần lượt là trung điểm của các đoạn thẳng OA, OB, OC.
a) Chứng minh Δ P Q R ∽ Δ A B C .
b) Cho biết Δ A B C có chu vi bằng 543cm, hãy tính chu vi Δ P Q R .
1cho tứ giác ABCD có 2 đương chéo vuông góc với nhau tại trung điểm O của chúng.CM
a/ tam giác ABC= tam giác ADC
b/ tính các góc của tứ giác ABCD biet rằng Góc ABO= 2BAO VÁ Góc C = 600
2. cho tu giac ABCD co diem O ở trong tứ giác gọi chu vi là 2p. CMR p<OA+OB+OC+OD<3p
Có : \(AB< OA+OB;BC< OB+OC;CD< OC+OD;DA< OD+OA\)
\(P_{ABCD}=2p=AB+BC+CD+DA< 2\left(OA+OB+OC+OD\right)\)
\(\Leftrightarrow\)\(p< OA+OB+OC+OD\)
Lại có : \(OA< AB-OB;OB< BC-OC;OC< CD-OD;OD< DA-OA\)
Cộng vế theo vế từng bđt trên ta được :
\(OA+OB+OC+OD< AB+BC+CD+DA-\left(OA+OB+OC+OD\right)\)
\(\Leftrightarrow\)\(2\left(OA+OB+OC+OD\right)< AB+BC+CD+DA\) (*)
Có tiếp -,- :
\(OA< AB+OB;OA< DA+OD\)\(\Rightarrow\)\(2OA< AB+DA+OB+OD\)
\(OB< AB+OA;OB< BC+OC\)\(\Rightarrow\)\(2OB< AB+BC+OA+OC\)
\(OC< BC+OB;OC< CD+OD\)\(\Rightarrow\)\(2OC< BC+CD+OB+OD\)
\(OD< CD+OC;OD< DA+OA\)\(\Rightarrow\)\(2OD< CD+DA+OC+OA\)
\(\Rightarrow\)\(2\left(OA+OB+OC+OD\right)< 2\left(AB+BC+CD+DA\right)+2\left(OA+OB+OC+OD\right)\)
\(< 2\left(AB+BC+CD+DA\right)+\left(AB+BC+CD+DA\right)\) ( kết hợp với (*) )
\(\Rightarrow\)\(2\left(OA+OB+OC+OD\right)< 3\left(AB+BC+CD+DA\right)\)
\(\Leftrightarrow\)\(OA+OB+OC+OD< 3.\frac{AB+BC+CD+DA}{2}=3.\frac{2p}{2}=3p\)
Vậy \(p< OA+OB+OC+OD< 3p\)
Đúng 0
Bình luận (0)
Cho tam giác ABC và điểm O nằm trong tam giác. Gọi M, N, P lần lượt là trung điểm của OA, OB, OC. Biết chu vi tam giác ABC là 5,5m. Tính chu vi tam giác MNP.
Xét ΔOAB có
M,N lần lượt là trung điểm của OA,OB
=>MN là đường trung bình của ΔOAB
=>\(MN=\dfrac{1}{2}AB\)
Xét ΔOAC có
M,P lần lượt là trung điểm của OA,OC
=>MP là đường trung bình của ΔOAC
=>\(MP=\dfrac{1}{2}AC\)
Xét ΔOBC có
N,P lần lượt là trung điểm của OB,OC
=>NP là đường trung bình của ΔOBC
=>\(NP=\dfrac{1}{2}BC\)
Chu vi tam giác MNP là:
MN+NP+MP
\(=\dfrac{1}{2}\left(AB+CA+BC\right)\)
\(=\dfrac{1}{2}\cdot5,5=2,75\left(m\right)\)
Đúng 0
Bình luận (0)