Cho em hỏi câu này vs ạ:
tìm m để
hàm số y=căn của 5+m+x xác định (-1;2 ]

Những câu hỏi liên quan
Cho em hỏi câu này vs ạ:
tìm m để
a)hàm số y=căn của 5+m+x xác định (-1;2 ]
b hàm số y=căn của x-m + 2x/căn của x-2m+1 xác định trên [-1;2 ]
c)hàm số y=5x+1/căn của x-m-1 + căn của 3m-x xác định trên (âm vc;-1 ]; [3,dương vc)
Cho hàm số y=(m-1)x-5
a) Xác định m để hàm số đồng biến, nghích biến
b) Xác định m để đồ thị hàm số đi qua diểm A(1;-3)
c) Vẽ đồ thị hàm số ứng với m tìm được ở câu b
Mọi người giúp mik vs mik sẽ tick cho các bạn nha
Mọi người giúp mk mấy bài trong ảnh vs thêm 3 câu trắc nghiệm này nhé( gkhi ghi đáp án trắc nghiệm, giải thích rõ giúp mk vs nhé!!!!!)1. Tìm m để hàm số y2x/(x-m) xác định với mọi x thuộc (0;1)A. m ≤ 0 ∨ m ≥ 1 B. m 0 ∨ m1C. m1 D. m02. Cho 2 tập hợp: A[2m-1; + ∞) ; B(- ∞;m+3]. A ∩B khác 0 khi và chỉ khi:A. m ≤4 B.m ≥3 C.m ≥-4 D. m ≥43. Cho 2 tập hợp: A[-1;3] ; B[m;m+5]. Để A ∩BA thì m thuộc tập nào sau đây:A.[-1;0]...
Đọc tiếp
Mọi người giúp mk mấy bài trong ảnh vs thêm 3 câu trắc nghiệm này nhé( gkhi ghi đáp án trắc nghiệm, giải thích rõ giúp mk vs nhé!!!!!)
1. Tìm m để hàm số y=2x/(x-m) xác định với mọi x thuộc (0;1)
A. m ≤ 0 ∨ m ≥ 1 B. m< 0 ∨ m>1
C. m<1 D. m>0
2. Cho 2 tập hợp: A=[2m-1; + ∞) ; B=(- ∞;m+3]. A ∩B khác 0 khi và chỉ khi:
A. m ≤4 B.m ≥3 C.m ≥-4 D. m ≥4
3. Cho 2 tập hợp: A=[-1;3] ; B=[m;m+5]. Để A ∩B=A thì m thuộc tập nào sau đây:
A.[-1;0] B.[-3;-2] C.[-2;-1] D.[1;2]
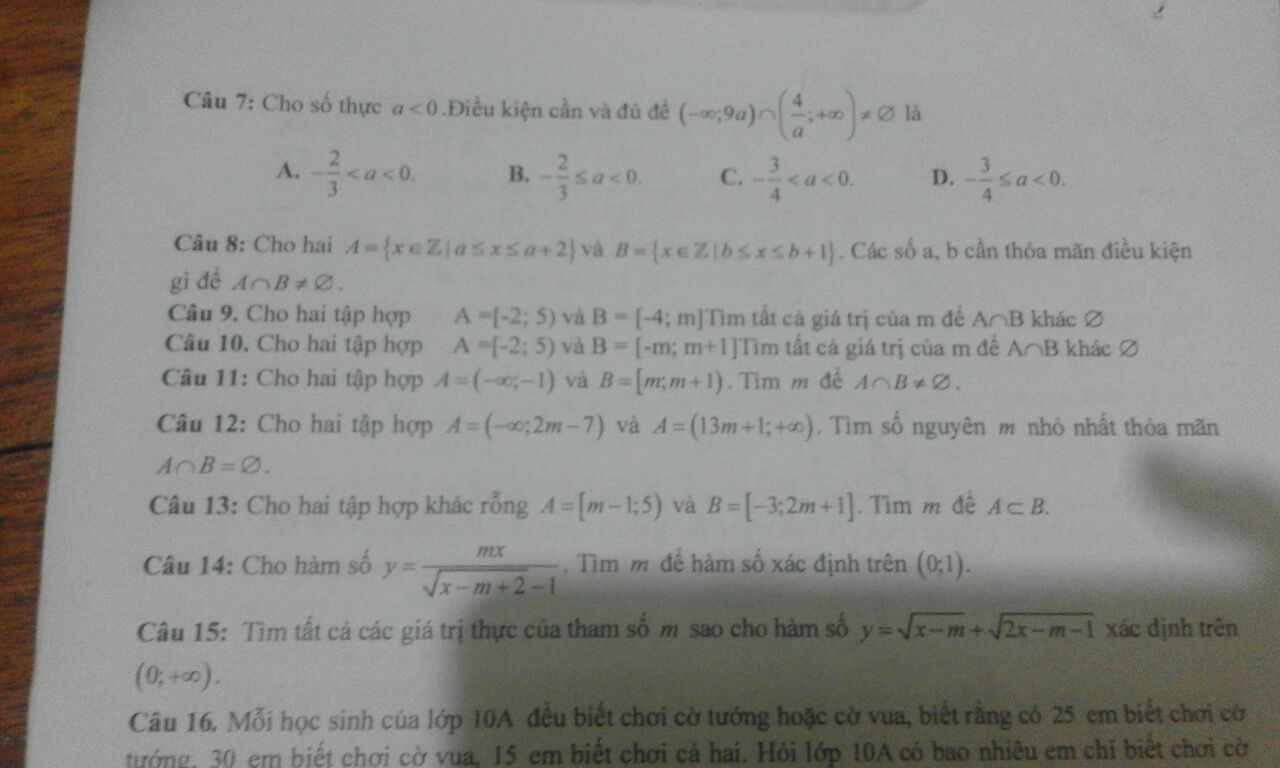 GIÚP MK VS!!! MAI MK PHẢI NỘP RỒI!!!!!!!!
GIÚP MK VS!!! MAI MK PHẢI NỘP RỒI!!!!!!!!
1.A. Ta thấy để hàm số xác định thì x-m\(\ne\)0 hay x\(\ne\)m mà vì x\(\in\)(0,1) nên để x\(\ne\)m thì m\(\notin\)(0,1)=>m>=1 hoặc m<=0
2A để A giao B khác 0 thì 2m-1<=m+3 hay m<=4
3C.A giao B =A khi \(\left\{{}\begin{matrix}m< =-1\\m+5>=3\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m< =1\\m>=-2\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Cho hàm số y=(m-1)x-5
a) Xác định m để hàm số đồng biến nghịch biến
b) Xác định m để đô thị hàm số đi qua điểm A(1;-3)
c) Vẽ đồ thị hàm số ứng với m tìm được ở câu b
Cho hàm số y=x³+mx²+2mx+3. Tìm điều kiện của m để hàm số đồng biến trên khoảng (0;2).

cho em hỏi y' là sao ạ em ko hiểu bài này
y' là đạo hàm bậc nhất của y. Bạn đọc sách toán phổ thông phần đạo hàm/ tìm max min của hàm số hoặc google search để tìm hiểu rõ hơn.
Đúng 0
Bình luận (0)
: Cho hàm số : y = (m – 5)x
⦁ Với giá trị nào của m thì hàm số đồng biến ? Nghịch biến ?
⦁ Xác định giá trị của m để đồ thị hàm số đi qua điểm A(1 ; 2)
⦁ Vẽ đồ thị hàm số đã tìm được ở câu b)
Để hàm số y=(m-5)x là hàm số bậc nhất thì \(m-5\ne0\)
hay \(m\ne5\)
1) Để hàm số y=(m-5)x đồng biến trên R thì m-5>0
hay m>5
Để hàm số y=(m-5)x nghịch biến trên R thì m-5<0
hay m<5
2) Để đồ thị hàm số y=(m-5)x đi qua A(1;2) thì
Thay x=1 và y=2 vào hàm số y=(m-5)x, ta được:
m-5=2
hay m=7(nhận)
Vậy: Để đồ thị hàm số y=(m-5)x đi qua A(1;2) thì m=7
Đúng 2
Bình luận (1)
3) cho hàm số bậc nhất \(y=\left(2-m\right)x+2m-1\) (d)
a) với m=1 hãy vẽ đồ thị
b) xác định m để (d) đi qua giao điểm của 2 đường thẳng \(y=-x+3\) và \(y=-2x+1\)
c) xác định m để (d) cắt đường thẳng \(y=x-2\) tại điểm có hoành độ -1
giúp mk vs ạ mk cần gấp
b: Phương trình hoành độ giao điểm là:
-x+3=-2x+1
\(\Leftrightarrow x=-2\)
Thay x=-2 vào y=-x+3, ta được;
y=2+3=5
Thay x=-2 và y=5 vào (d), ta được:
\(-2\left(2-m\right)+2m-1=5\)
\(\Leftrightarrow2m-4+2m-1=5\)
\(\Leftrightarrow4m=10\)
hay \(m=\dfrac{5}{2}\)
Đúng 0
Bình luận (0)
Cho hàm số y = (3 – m)x2a) Tìm điều kiện của m để hàm số trên được xác định.b) Xác định m để hàm số đồng biến với mọi x < 0.c) Xác định m để y = 0 là giá trị nhỏ nhất của hàm số tại x = 0.
a, ĐKXĐ để hàm được xác định : \(3-m\ne0\)
\(\Leftrightarrow m\ne3\)
b, - Với x < 0 để hàm số đồng biến thì : \(3-m< 0\)
\(\Leftrightarrow m>3\)
Vậy ...
c, - Để y = 0 là giá trị nhỏ nhất của hàm số tại x = 0
\(\Leftrightarrow a>0\)
\(\Leftrightarrow3-m>0\)
\(\Leftrightarrow m< 3\)
Vậy ...
Đúng 2
Bình luận (0)
a) Để hàm số \(y=\left(3-m\right)x^2\) được xác định thì \(3-m\ne0\)
hay \(m\ne3\)
b) Để hàm số \(y=\left(3-m\right)x^2\) đồng biến với mọi x<0 thì \(3-m< 0\)
\(\Leftrightarrow m>3\)
c) Để y=0 là giá trị nhỏ nhất của hàm số tại x=0 thì 3-m>0
hay m<3
Đúng 2
Bình luận (0)
Cho hàm số: y = (m - 2).x2
1) Xác định m để đồ thị hàm số đi qua điểm A( -2; -2)
2) Tìm tọa độ giao điểm M và N của đồ thị hàm số ở câu 1) với đường thẳng có phương trình y = -1
Lời giải:
1. Để đths đi qua $A(-2;-2)$ thì:
$y_A=(m-2)x_A^2$
$\Leftrightarrow -2=(m-2)(-2)^2$
$\Leftrightarrow m-2=\frac{-1}{2}$
$\Leftrightarrow m=\frac{3}{2}$
2.
PT hoành độ giao điểm của đths câu 1 với $y=-1$ là:
$(\frac{3}{2}-2)x^2=-1$
$\Leftrightarrow \frac{-1}{2}x^2=-1$
$\Leftrightarrow x^2=2$
$\Leftrightarrow x=\pm \sqrt{2}$
Vậy 2 tọa độ giao điểm là $M(\sqrt{2}; -1); (-\sqrt{2}; -1)$
Đúng 1
Bình luận (0)













