Cho hình vẽ.Biết AB//DC và AD//BC.
Chứng minh rằng A=C
Những câu hỏi liên quan
Cho ABC vuông tại A có BD là phân giác, kẻ DE BC (E BC). Gọi F là giao điểm của AB và DE. Chứng minh rằng: a/ BD là trung trực của AE b/ DF = DC c/ AD c/ AD<DC d/ AE//FC vẽ hình vs ạ
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
=>BA=BE và DA=DE
=>BD là trung trực của AE
b: Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
góc ADF=góc EDC
=>ΔDAF=ΔDEC
=>DF=DC
c; AD=DE
DE<DC
=>AD<DC
d: BA/AF=BE/EC
=>AE//FC
Đúng 0
Bình luận (0)
Cho ABC vuông tại A có BD là phân giác, kẻ DE BC (E BC). Gọi F là giao điểm của AB và DE. Chứng minh rằng: a/ BD là trung trực của AE b/ DF = DC c/ AD c/ AD<DC d/ AE//FC vẽ hình vs ạ
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
=>BA=BE và DA=DE
=>BD là trung trực của AE
b: Xet ΔDAF vuông tại A và ΔDEC vuông tạiE có
DA=DE
góc ADF=góc EDC
=>ΔDAF=ΔDEC
=>DF=DC
c: AD=DE
mà DE<DC
nên AD<CD
d: Xét ΔBFC có BA/AF=BE/EC
nên AE//FC
Đúng 1
Bình luận (0)
Cho tứ giác ABCD có AB=DC;AD=BC chứng minh rằng AB//DC;AD//BC
Ta có:AB=CD (gt)
AD=BC (gt)
=> Tứ giác ABCD là hình bình hành ( tứ giác có 2 cặp cạnh đối bằng nhau là hình bình hành)
=>AB//CD( tính chất hình bình hành) và AD//BC ( tính chất hình bình hành)
Đúng 0
Bình luận (0)
Cho hình thang cân ABCD (AB//CD, AB<CD) có AB=AD. chứng minh rằng DC-AB<AD+BC
Qua P kẻ đường thẳng song song với AD cắt CD tại P. Khi đó dễ thấy \(AB=DP\). Từ đó \(DC-AB=DC-DM=CM\)
Mặt khác, \(AD=BM\) nên \(AD+BC=BM+BC\).
Hiển nhiên \(CM< BM+BC\). Điều này dẫn đến \(DC-AB< AD+BC\) (đpcm)
Đúng 2
Bình luận (0)
Cho hình thang ABCD (AB // CD).
Đường thẳng a song song với DC, cắt các cạnh AD và BC theo thứ tự tại E và F. Chứng minh rằng:
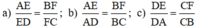
cho tứ giác abcd có a+d=180 d>c và ab<dc chứng minh rằng ad<bc
cho tứ giác abcd có a+d=180 d>c và ab<dc chứng minh rằng ad<bc
cho tứ giác abcd có a+d=180 d>c và ab<dc chứng minh rằng ad<bc
Cho hình thang cân ABCD(AB//CD), AB=BC và BC vuông góc với BD
a) Chứng minh AC vuông góc với AD
b) Tính số đo các góc hình thang
c) Gọi O là giao điểm của 2 đường chéo. Chứng minh rằng O cách đều 2 cnhj bên và đáy lớn
d) Gọi M là giao điểm cảu AD và Bc. H là hình chiếu của O trên DC. Chứng minh M,H,O thẳng hàng